Table of Contents:

分布式散列表（DHT），用来将一个关键值（key）的集合分散到所有在分布式系统中的节点，比较有名的实现有Chord（一致性哈希），Kademlia（被应用在BitTorrent，电骡，I2P ，以太坊等P2P网络实现中）
Kademlia算法是一种分布式存储及路由的算法。什么是分布式存储？试想一下，一所1000人的学校，现在学校突然决定拆掉图书馆（不设立中心化的服务器），将图书馆里所有的书都分发到每位学生手上（所有的文件分散存储在各个节点上）。即是所有的学生，共同组成了一个分布式的图书馆。
我的理解：在无中心节点条件下协调大量离散节点完成操作（增，删，定位，存储数据）的协议系统，这也是P2P网络的核心吧

论文：http://pdos.csail.mit.edu/~petar/papers/maymounkov-kademlia-lncs.pdf

概念

拓扑结构——二叉树

散列值的预处理

Kad 也采用了node ID 与 data key 同构的设计思路。然后 Kad 采用某种算法把 key 映射到一个二叉树，每一个 key 都是这个二叉树的【叶子】，每个 leaf 节点都表示一个 Peer。
在映射之前，先做一下预处理。
1. 先把 key 以二进制形式表示。
2. 把每一个 key 缩短为它的【最短唯一前缀】,也就是通过前缀就可以唯一的区别一个key，而前缀后面的信息就没啥用了。

比如：

10110  -> 101
10010  -> 100
01011  -> 01

为啥要搞“最短唯一前缀”？

Kad 使用 160比特 的散列算法（比如 SHA1），完整的 key 用二进制表示有 160 个数位（bit）。
首先，实际运行的 Kad 网络，即使有几百万个节点，相比 keyspace（2^160）也只是很小很小很小的一个子集。
其次，由于散列函数的特点，key 的分布是【高度随机】的。因此也是【高度离散】的——任何两个 key 都【不会】非常临近。
所以，使用“最短唯一前缀”来处理 key 的二进制形式，得到的结果就会很短（比特数远远小于 160）。

散列值的映射

完成上述的预处理后，接下来的映射规则是（本质是根据最长前缀划分）：
1. 先把 key 以二进制形式表示，然后从高位到低位依次处理。
2. 二进制的第 n 个 bit 就对应了二叉树的第 n 层
3. 如果该位是 1，进入左子树，是 0 则进入右子树（这只是人为约定，反过来处理也可以）
4. 全部数位都处理完后，这个 key 就对应了二叉树上的某个【叶子】



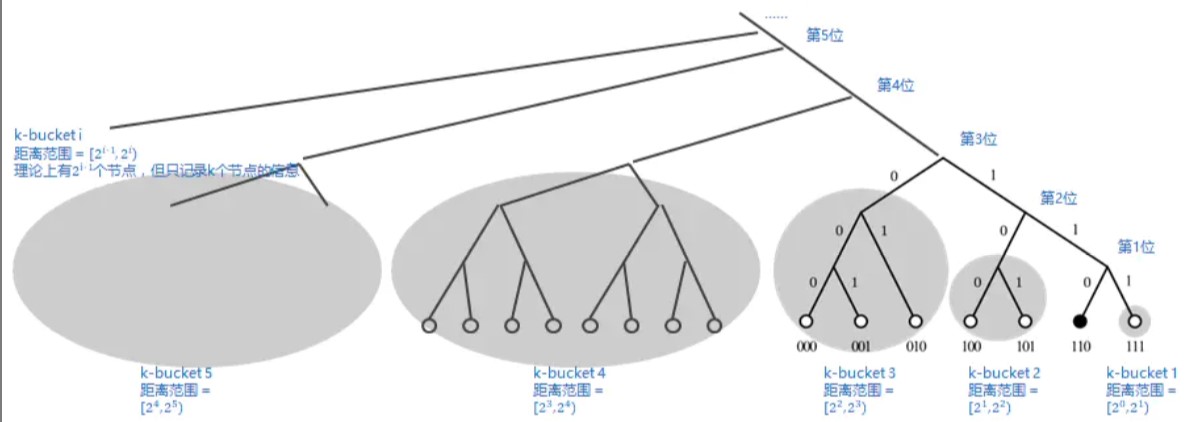
路由机制

二叉树的拆分

对每一个节点，都可以【按照自己的视角】对整个二叉树进行拆分。
拆分的规则是：先从根节点开始，把【不包含】自己的那个子树拆分出来；然后在剩下的子树再拆分不包含自己的下一层子树；以此类推，直到最后只剩下自己。
Kad 默认的散列值空间是 m = 160（散列值有 160 bits），因此拆分出来的子树【最多】有 160 个（考虑到实际的节点数【远远小于】2^160，子树的个数会明显小于 160）。每个子树对应着一个Bucket。
对于每一个节点而言，当它以自己的视角完成子树拆分后，会得到 n 个子树；对于每个子树，如果它都能知道里面的一个节点，那么它就可以利用这 n 个节点进行递归路由，从而到达整个二叉树的【任何一个】节点
每个子树是一个k-bucket， 可以通过XOR的结果来索引，具体公式为判断距离落在那个区间，[2^i, 2^(i+1))

另一种二叉树拆分的视角

Kademlia 中，根据当前节点的 Node ID 与它保存的其他 peer 节点 Node ID 的匹配的最多的前缀个数来构建一颗二叉树（Binary Tree），这里前缀匹配的 bit 数也叫 LCP，Longest Common Prefix，从上面的运算我们可以观察到，当前节点 1101 与 1000 的前缀只有最高位是匹配的。因此，其LCP 就是 1。Kademlia 中根据 LCP 来划分子树。当前节点的每个 LCP 都是一个子树。

K-桶（K-bucket）

Kademlia 中把子树中包含的 leaf 节点数量被设置为最多 k 个。这样可以有效控制整棵树的膨胀。
前面说了，每个节点在完成子树拆分后，只需要知道每个子树里面的一个节点，就足以实现全遍历。但是考虑到健壮性（请始终牢记：分布式系统的节点是动态变化滴），光知道【一个】显然是不够滴，需要知道【多个】才比较保险。
所以 Kad 论文中给出了一个“K-桶（K-bucket）”的概念。也就是说：每个节点在完成子树拆分后，要记录每个子树里面的 K 个节点。这里所说的 K 值是一个【系统级】的常量。由使用 Kad 的软件系统自己设定（比如 BT 下载使用的 Kad 网络，K 设定为 8）。
这个“K-桶”其实就是【路由表】。对于某个节点而言，如果【以它自己为视角】拆分了 n 个子树，那么它就需要维护 n 个路由表，并且每个路由表的【上限】是 K。

K-桶（K-bucket）的刷新机制

节点可能是频繁加入和退出网络的，所以要刷新
刷新机制大致有如下几种：
1. 主动收集节点
任何节点都可以主动发起“查询节点”的请求（对应于协议类型 FIND_NODE），从而刷新 K 桶中的节点信息
2. 被动收集节点
如果收到其它节点发来的请求（协议类型 FIND_NODE 或 FIND_VALUE），会把对方的 ID 加入自己的某个 K 桶中。
3. 探测失效节点
Kad 还是支持一种探测机制（协议类型 PING），可以判断某个 ID 的节点是否在线。因此就可以定期探测路由表中的每一个节点，然后把下线的节点从路由表中干掉。

当需要更新一个 kbucket，时取决于两个因素：
* kbucket 未满，则直接添加
* kbucket 已满，则判断是否存在剔除失效节点，存在，则用新节点替换，不存在，则抛弃新节点。

“并发请求”与“α 参数”

“K桶”的这个设计思路【天生支持并发】。因为【同一个】“K桶”中的每个节点都是平等的，没有哪个更特殊；而且对【同一个】“K桶”中的节点发起请求，互相之间没有影响（无耦合）。
所以 Kad 协议还引入了一个“α参数/α因子”，默认设置为 3，使用 Kad 的软件可以在具体使用场景中调整这个“α因子”。
当需要路由到某个“子树”，会从该子树对应的“K桶”中挑选【α个节点】，然后对这几个节点【同时】发出请求。

节点的加入

1. 任何一个新来的节点（假设叫 A），需要先跟 DHT 中已有的任一节点（假设叫 B）建立连接。
2. A 随机生成一个散列值作为自己的 ID（对于足够大的散列值空间，ID 相同的概率忽略不计）
3. A 向 B 发起一个查询请求（协议类型 FIND_NODE），请求的 ID 是自己（通俗地说，就是查询自己）
4. B 收到该请求之后，（如前面所说）会先把 A 的 ID 加入自己的某个 K 桶中。
然后，根据 FIND_NODE 协议的约定，B 会找到【K个】最接近 A 的节点，并返回给 A。
（B 怎么知道哪些节点接近 A 捏？这时候，【用 XOR 表示距离】的算法就发挥作用啦）
5. A 收到这 K 个节点的 ID 之后，（仅仅根据这批 ID 的值）就可以开始初始化自己的 K 桶。
6. 然后 A 会继续向刚刚拿到的这批节点发送查询请求（协议类型 FIND_NODE），如此往复（递归），直至 A 建立了足够详细的路由表。

节点的退出

与 Chord 不同，Kad 对于节点退出没有额外的要求（没有“主动退出”的说法）。
所以，Kad 的节点想离开 DHT 网络【不】需要任何操作（套用徐志摩的名言：悄悄的我走了，正如我悄悄的来）

如何找到某个节点

算法的设计是，如果一个节点离你越近，你手上的k桶里存有ta的地址的概率越大，原因是离自己越近的节点，节点的数量就越少，所有存在的概率就越大。而算法的核心的思路就可以是：当你知道目标节点A与你之间的距离，你可以在你的k桶上先找到一个你认为与节点A最相近的节点B，请节点B再进一步去查找节点A的地址。
其原理就是在其划分的二叉树上不断的缩小范围，一次至少可以缩写一半。

Kademlia 协议操作类型

Kademlia 协议包括四种远程 RPC 操作：PING、STORE、FIND_NODE、FIND_VALUE。
1. PING 操作的作用是探测一个节点，用以判断其是否仍然在线。
2. STORE 操作的作用是通知一个节点存储一个 <key,value> 对，以便以后查询需要。
3. FIND_NODE 操作使用一个 160 bit 的 ID 作为参数。本操作的接受者返回它所知道的更接近目标 ID 的 K 个节点的 (IP address, UDP port, Node ID) 信息。
这些节点的信息可以是从一个单独的 K 桶获得，也可以从多个 K 桶获得（如果最接近目标 ID 的 K 桶未满）。不管是哪种情况，接受者都将返回 K 个节点的信息给操作发起者。但如果接受者所有 K 桶的节点信息加起来也没有 K 个，则它会返回全部节点的信息给发起者。
4. FIND_VALUE 操作和 FIND_NODE 操作类似，不同的是它只需要返回一个节点的 (IP address, UDP port, Node ID) 信息。如果本操作的接受者收到同一个 key 的 STORE 操作，则会直接返回存储的 value 值。

Kademlia的实现

Kademlia 算法在不同的项目中会有不同的实现，区别主要在于 kbucket 数据结构及其相关方法。
比如，典型的 Kademlia 实现是，先根据 ID 空间预先分配 kbucket 数量的空间（比如 160 位，就分配 160 个 buckets 空间，256 位就直接分配 256 个 buckets 空间，这样，后续计算 distance 的时候可以直接 distance 作为 bucket 索引），还有就是 IPFS 这种，也是原始 Kademlia 论文中提到的.
动态分配 buckets，如果节点少的时候，就只有一个 bucket，当节点不断增加之后，原 bucket 不断分裂，具体就是，每次满了 k 个元素，原 bucket 就分裂成 2 个。这样的话，对于内存空间是一个优化。而以太坊中的实现又略有不同，它使用固定数量的 buckets，但是却限定在 17 个，而不是 256 个，它通过一个 log 映射表来把新节点均匀分布在各个 buckets 中。

参考链接

穿网