Table of Contents:

05 | 计算机指令：让我们试试用纸带编程

在软硬件接口中，CPU 帮我们做了什么事？

从硬件的角度来看，CPU 就是一个超大规模集成电路，通过电路实现了加法、乘法乃至各种各样的处理逻辑。
如果我们从软件工程师的角度来讲，CPU 就是一个执行各种计算机指令（Instruction Code）的逻辑机器。
这里的计算机指令，就好比一门 CPU 能够听得懂的语言，我们也可以把它叫作机器语言（Machine Language）。

不同的 CPU 能够听懂的语言不太一样。比如，我们的个人电脑用的是 Intel 的 CPU，苹果手机用的是 ARM 的 CPU。
这两者能听懂的语言就不太一样。类似这样两种 CPU 各自支持的语言，就是两组不同的计算机指令集，英文叫 Instruction Set。

汇编代码其实就是给程序员看的机器码

从编译到汇编，代码怎么变成机器码？

// test.c
int main()
{
  int a = 1;
  int b = 2;
  a = a + b;
}

$ gcc -g -c test.c
$ objdump -d -M intel -S test.o

// 输出为以下格式
test.o:     file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <main>:
int main()
{
   0:   55                      push   rbp
   1:   48 89 e5                mov    rbp,rsp
  int a = 1;
   4:   c7 45 fc 01 00 00 00    mov    DWORD PTR [rbp-0x4],0x1
  int b = 2;
   b:   c7 45 f8 02 00 00 00    mov    DWORD PTR [rbp-0x8],0x2
  a = a + b;
  12:   8b 45 f8                mov    eax,DWORD PTR [rbp-0x8]
  15:   01 45 fc                add    DWORD PTR [rbp-0x4],eax
}
  18:   5d                      pop    rbp
  19:   c3                      ret

解析指令和机器码

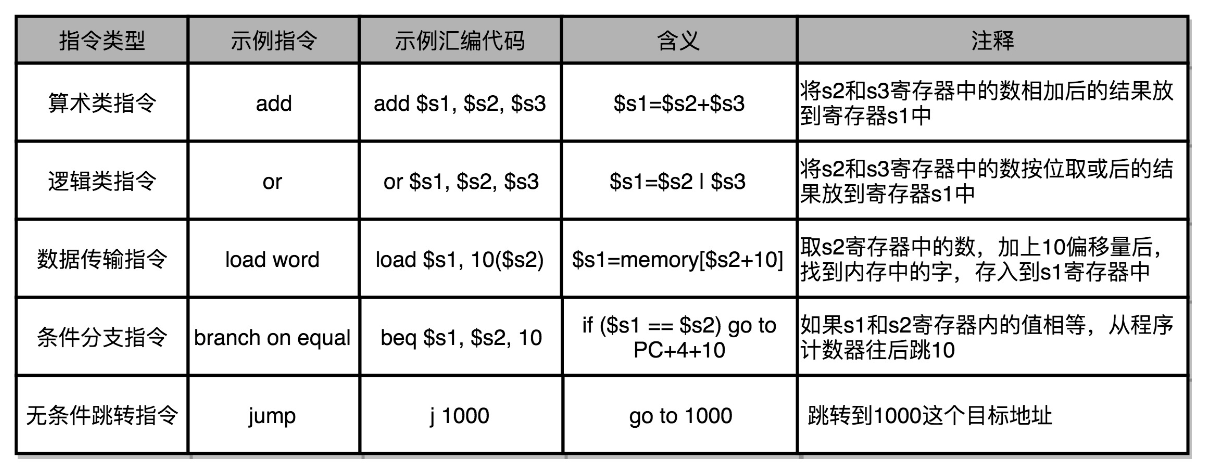
我们日常用的 Intel CPU，有 2000 条左右的 CPU 指令，实在是太多了,常见的指令可以分成五大类。

MIPS 是一组由 MIPS 技术公司在 80 年代中期设计出来的 CPU 指令集。就在最近，MIPS 公司把整个指令集和芯片架构都完全开源了。

这一讲里，我们看到了一个 C 语言程序，是怎么被编译成为汇编语言，乃至通过汇编器再翻译成机器码的。
除了 C 这样的编译型的语言之外，不管是 Python 这样的解释型语言，还是 Java 这样使用虚拟机的语言，其实最终都是由不同形式的程序，把我们写好的代码，转换成 CPU 能够理解的机器码来执行的。

06 | 指令跳转：原来if...else就是goto

CPU 是如何执行指令的？


一个 CPU 里面会有很多种不同功能的寄存器。如下：
1. PC 寄存器（Program Counter Register），我们也叫指令地址寄存器（Instruction Address Register）。顾名思义，它就是用来存放下一条需要执行的计算机指令的内存地址。
2. 指令寄存器（Instruction Register），用来存放当前正在执行的指令。
3. 条件码寄存器（Status Register），用里面的一个一个标记位（Flag），存放 CPU 进行算术或者逻辑计算的结果。
4. 通用寄存器，有些寄存器既可以存放数据，又能存放地址，我们就叫它通用寄存器。

一个程序执行的时候，CPU 会根据 PC 寄存器里的地址，从内存里面把需要执行的指令读取到指令寄存器里面执行，然后根据指令长度自增，开始顺序读取下一条指令。可以看到，一个程序的一条条指令，在内存里面是连续保存的，也会一条条顺序加载。
而有些特殊指令，比如上一讲我们讲到 J 类指令，也就是跳转指令，会修改 PC 寄存器里面的地址值。这样，下一条要执行的指令就不是从内存里面顺序加载的了。

从 if…else 来看程序的执行和跳转

  if (r == 0)
  {
    a = 1;
  } else {
    a = 2;
  }
//====================
    if (r == 0)
  3b:   83 7d fc 00             cmp    DWORD PTR [rbp-0x4],0x0   #进行比较，然后结果放到条件寄存器中
  3f:   75 09                   jne    4a <main+0x4a>   # jump not equal,若真，跳到else分支
    {
        a = 1;
  41:   c7 45 f8 01 00 00 00    mov    DWORD PTR [rbp-0x8],0x1
  48:   eb 07                   jmp    51 <main+0x51>   # 跳到else分支末尾
    }
    else
    {
        a = 2;
  4a:   c7 45 f8 02 00 00 00    mov    DWORD PTR [rbp-0x8],0x2
  51:   b8 00 00 00 00          mov    eax,0x0    # 表示一个占位符，供跳转用
    }

如何通过 if…else 和 goto 来实现循环？

    int a = 0;
    for (int i = 0; i < 3; i++)
    {
        a += i;
    }
//=======================
    for (int i = 0; i < 3; i++)
   b:   c7 45 f8 00 00 00 00    mov    DWORD PTR [rbp-0x8],0x0
  12:   eb 0a                   jmp    1e <main+0x1e>
    {
        a += i;
  14:   8b 45 f8                mov    eax,DWORD PTR [rbp-0x8]
  17:   01 45 fc                add    DWORD PTR [rbp-0x4],eax
    for (int i = 0; i < 3; i++)
  1a:   83 45 f8 01             add    DWORD PTR [rbp-0x8],0x1
  1e:   83 7d f8 02             cmp    DWORD PTR [rbp-0x8],0x2
  22:   7e f0                   jle    14 <main+0x14>  # jump less equal，满足循环条件就跳到上边，从而达到重复执行一段代码的目的
  24:   b8 00 00 00 00          mov    eax,0x0
    }

其实，你有没有觉得，jle 和 jmp 指令，有点像程序语言里面的 goto 命令，直接指定了一个特定条件下的跳转位置。
虽然我们在用高级语言开发程序的时候反对使用 goto，但是实际在机器指令层面，无论是 if…else…也好，还是 for/while 也好，都是用和 goto 相同的跳转到特定指令位置的方式来实现的。

07 | 函数调用：为什么会发生stack overflow？

int static add(int a, int b)
{
    return a+b;
}
int main()
{
    int x = 5;
    int y = 10;
    int u = add(x, y);
}

//============================
int static add(int a, int b)
{
   0:   55                      push   rbp    //入栈
   1:   48 89 e5                mov    rbp,rsp
   4:   89 7d fc                mov    DWORD PTR [rbp-0x4],edi
   7:   89 75 f8                mov    DWORD PTR [rbp-0x8],esi
    return a+b;
   a:   8b 55 fc                mov    edx,DWORD PTR [rbp-0x4]
   d:   8b 45 f8                mov    eax,DWORD PTR [rbp-0x8]
  10:   01 d0                   add    eax,edx
}
  12:   5d                      pop    rbp  //出栈
  13:   c3                      ret
0000000000000014 <main>:
int main()
{
  14:   55                      push   rbp
  15:   48 89 e5                mov    rbp,rsp
  18:   48 83 ec 10             sub    rsp,0x10
    int x = 5;
  1c:   c7 45 fc 05 00 00 00    mov    DWORD PTR [rbp-0x4],0x5
    int y = 10;
  23:   c7 45 f8 0a 00 00 00    mov    DWORD PTR [rbp-0x8],0xa
    int u = add(x, y);
  2a:   8b 55 f8                mov    edx,DWORD PTR [rbp-0x8]
  2d:   8b 45 fc                mov    eax,DWORD PTR [rbp-0x4]
  30:   89 d6                   mov    esi,edx
  32:   89 c7                   mov    edi,eax
  34:   e8 c7 ff ff ff          call   0 <add>   // 其实是跳转到add函数的地址
  39:   89 45 f4                mov    DWORD PTR [rbp-0xc],eax
  3c:   b8 00 00 00 00          mov    eax,0x0
}
  41:   c9                      leave
  42:   c3                      ret

我们在调用第 34 行的 call 指令时，会把当前的 PC 寄存器里的下一条指令的地址压栈，保留函数调用结束后要执行的指令地址。而 add 函数的第 0 行，push rbp 这个指令，就是在进行压栈。这里的 rbp 又叫栈帧指针（Frame Pointer），是一个存放了当前栈帧位置的寄存器。push rbp 就把之前调用函数，也就是 main 函数的栈帧的栈底地址，压到栈顶。

栈中最主要的两个寄存器是rbp和rsp，分别指向栈底和栈顶。参考[[ProgrammingGroundUp笔记]]中的函数调用

stack layout
    Parameter #N     <--- N*4+4(%ebp)
    ...              
    Parameter 2      <--- 12(%ebp)
    Parameter 1      <--- 8(%ebp)
    Return Address   <--- 4(%ebp)
    Old %ebp         <--- (%ebp)
    Local Variable 1 <--- -4(%ebp)
    Local Variable 2 <--- -8(%ebp) and (%esp)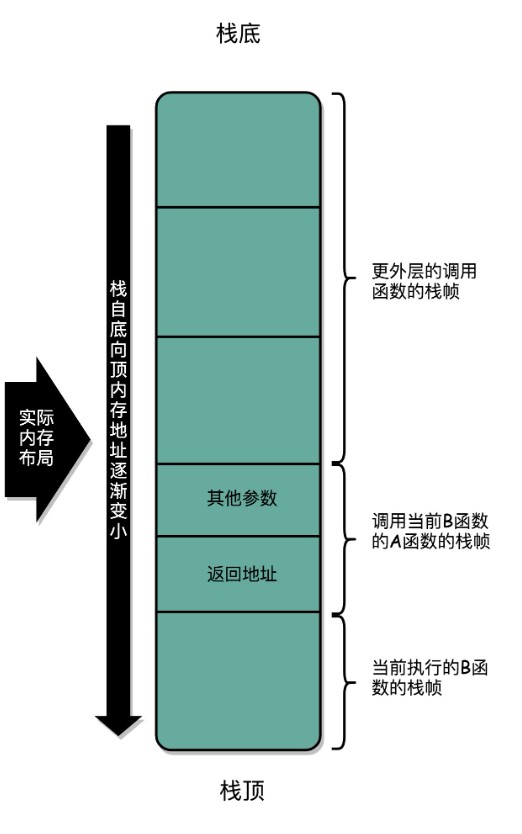

stack overflow
除了无限递归，递归层数过深，在栈空间里面创建非常占内存的变量（比如一个巨大的数组），这些情况都很可能给你带来 stack overflow。

如何利用函数内联进行性能优化？

上面我们提到一个方法，把一个实际调用的函数产生的指令，直接插入到的位置，来替换对应的函数调用指令。尽管这个通用的函数调用方案，被我们否决了，但是如果被调用的函数里，没有调用其他函数，这个方法还是可以行得通的。

这样没有调用其他函数，只会被调用的函数，我们一般称之为叶子函数（或叶子过程）

事实上，这就是一个常见的编译器进行自动优化的场景，我们通常叫函数内联（Inline）。我们只要在 GCC 编译的时候，加上对应的一个让编译器自动优化的参数 -O，编译器就会在可行的情况下，进行这样的指令替换。

内联带来的优化是，CPU 需要执行的指令数变少了，根据地址跳转的过程不需要了，压栈和出栈的过程也不用了。
不过内联并不是没有代价，内联意味着，我们把可以复用的程序指令在调用它的地方完全展开了。如果一个函数在很多地方都被调用了，那么就会展开很多次，整个程序占用的空间就会变大了。

08 | ELF和静态链接：为什么程序无法同时在Linux和Windows下 运行？

编译、链接和装载：拆解程序执行

“C 语言代码 - 汇编代码 - 机器码” 这个过程，在我们的计算机上进行的时候是由两部分组成的。
第一个部分由编译（Compile）、汇编（Assemble）以及链接（Link）三个阶段组成。在这三个阶段完成之后，我们就生成了一个可执行文件。

第二部分，我们通过装载器（Loader）把可执行文件装载（Load）到内存中。CPU 从内存中读取指令和数据，来开始真正执行程序。

ELF 格式和链接：理解链接过程

ELF格式
在 Linux 下，可执行文件和目标文件所使用的都是一种叫ELF（Execuatable and Linkable File Format）的文件格式，这里面不仅存放了编译成的汇编指令，还保留了很多别的数据。

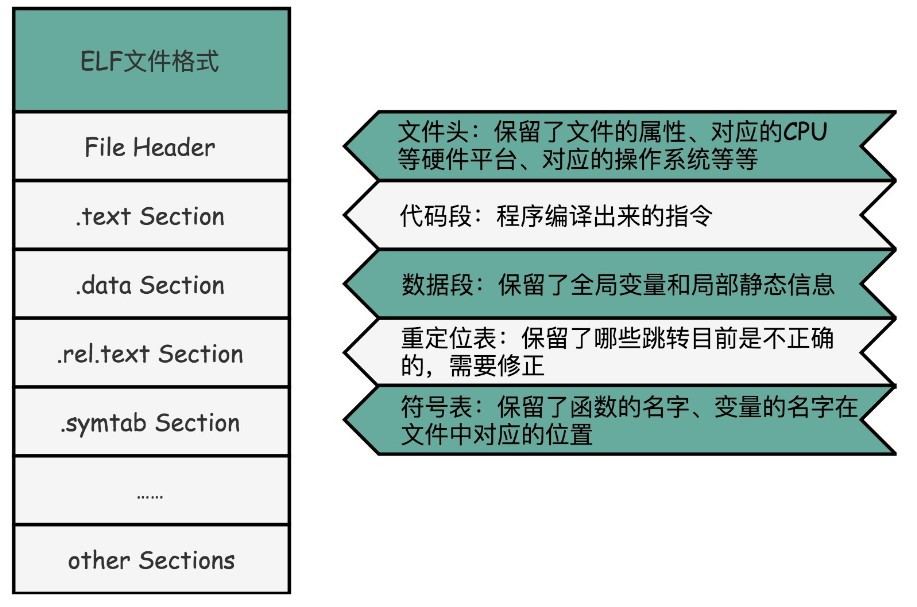
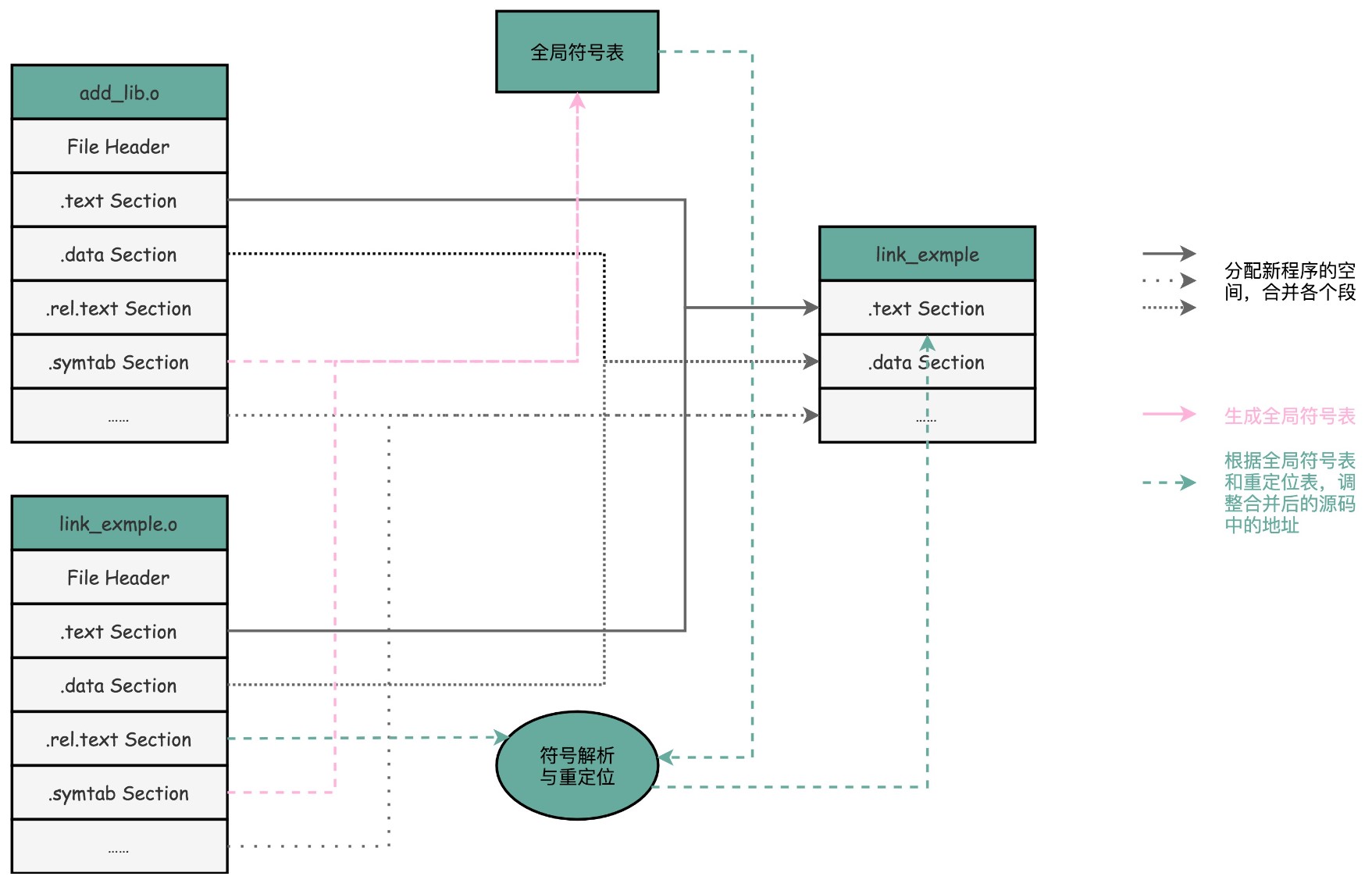
链接器执行的过程
链接器会扫描所有输入的目标文件，然后把所有符号表里的信息收集起来，构成一个全局的符号表。然后再根据重定位表，把所有不确定要跳转地址的代码，根据符号表里面存储的地址，进行一次修正。最后，把所有的目标文件的对应段进行一次合并，变成了最终的可执行代码。这也是为什么，可执行文件里面的函数调用的地址都是正确的。
在链接器把程序变成可执行文件之后，要装载器去执行程序就容易多了。
装载器不再需要考虑地址跳转的问题，只需要解析 ELF 文件，把对应的指令和数据，加载到内存里面供 CPU执行就可以了。

我们今天讲的是 Linux 下的 ELF 文件格式，而 Windows 的可执行文件格式是一种叫作PE（Portable Executable Format）的文件格式。Linux 下的装载器只能解析 ELF 格式而不能解析 PE 格式。
如果我们有一个可以能够解析 PE 格式的装载器，我们就有可能在 Linux 下运行 Windows程序了。这样的程序真的存在吗？
没错，Linux 下著名的开源项目 Wine，就是通过兼容PE 格式的装载器，使得我们能直接在 Linux 下运行 Windows 程序的。而现在微软的Windows 里面也提供了 WSL，也就是 Windows Subsystem for Linux，可以解析和加载ELF 格式的文件。

09 | 程序装载：“640K内存”真的不够用么？

程序装载面临的挑战

装载主要面临的其实是一个内存的问题。

装载器需要满足两个要求：
第一，可执行程序加载后占用的内存空间应该是连续的。我们在第 6 讲讲过，执行指令的时候，程序计数器是顺序地一条一条指令执行下去。这也就意味着，这一条条指令需要连续地存储在一起。
第二，我们需要同时加载很多个程序，并且不能让程序自己规定在内存中加载的位置。

虚拟内存

每个程序在自己来看都拥有连续的地址空间，独占整个操作的内存。
我们把指令里用到的内存地址叫作虚拟内存地址（Virtual Memory Address），实际在内存硬件里面的空间地址，我们叫物理内存地址（Physical Memory Address）**。

程序里有指令和各种内存地址，我们只需要关心虚拟内存地址就行了。对于任何一个程序来说，它看到的都是同样的内存地址,比如说都是从某个固定地址开始的地址，而它编译的程序中是不可能知道程序中的物理地址的，因为你不知道程序会被装载到哪里。我们维护一个虚拟内存到物理内存的映射表，这样实际程序指令执行的时候，会通过虚拟内存地址，找到对应的物理内存地址，然后执行。

内存分段

这种找出一段连续的物理内存和虚拟内存地址进行映射的方法，我们叫分段（Segmentation）**。

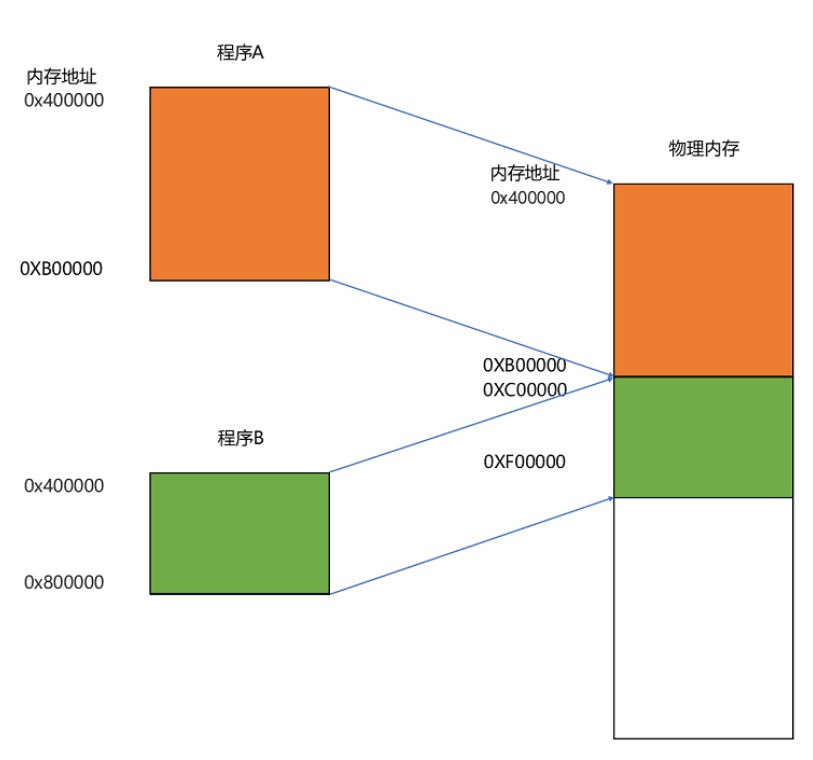
内存交换（Memory Swapping）:把内存中的程序load到硬盘中，等到需要的时候再load到内存中。
虚拟内存、分段，再加上内存交换，看起来似乎已经解决了计算机同时装载运行很多个程序的问题。不过，你千万不要大意，这三者的组合仍然会遇到一个性能瓶颈。硬盘的访问速度要比内存慢很多，而每一次内存交换，我们都需要把一大段连续的内存数据写到硬盘上。所以，如果内存交换的时候，交换的是一个很占内存空间的程序，这样整个机器都会显得卡顿。

内存分页

既然问题出在内存碎片和内存交换的空间太大上，那么解决问题的办法就是，当需要进行内存交换的时候，让需要交换写入或者从磁盘装载的数据更少一点，这样就可以解决这个问题。这个办法，在现在计算机的内存管理里面，就叫作内存分页（Paging）。
和分段这样分配一整段连续的空间给到程序相比，分页是把整个物理内存空间切成一段段固定尺寸的大小。而对应的程序所需要占用的虚拟内存空间，也会同样切成一段段固定尺寸的大小。这样一个连续并且尺寸固定的内存空间，我们叫页（Page）。从虚拟内存到物理内存的映射，不再是拿整段连续的内存的物理地址，而是按照一个一个页来的。页的尺寸一般远远小于整个程序的大小。在 Linux 下，我们通常只设置成 4KB。你可以通过命令看看你手头的 Linux 系统设置的页的大小。

当要读取特定的页，却发现数据并没有加载到物理内存里的时候，就会触发一个来自于 CPU 的缺页错误（Page Fault）。我们的操作系统会捕捉到这个错误，然后将对应的页，从存放在硬盘上的虚拟内存里读取出来，加载到物理内存里。这种方式，使得我们可以运行那些远大于我们实际物理内存的程序。

在虚拟内存、内存交换和内存分页这三者结合之下，你会发现，其实要运行一个程序，“必需”的内存是很少的。CPU 只需要执行当前的指令，极限情况下，内存也只需要加载一页就好了。再大的程序，也可以分成一页。每次，只在需要用到对应的数据和指令的时候，从硬盘上交换到内存里面来就好了。以我们现在 4K 内存一页的大小，640K 内存也能放下足足 160 页呢，也无怪乎在比尔·盖茨会说出“640K ought to be enough for anyone”这样的话。
不过呢，硬盘的访问速度比内存慢很多，所有大内存还是很有用的。

10 | 动态链接：程序内部的“共享单车”

链接可以分动、静，共享运行省内存

在动态链接的过程中，我们想要“链接”的，不是存储在硬盘上的目标文件代码，而是加载到内存中的共享库（Shared Libraries）。

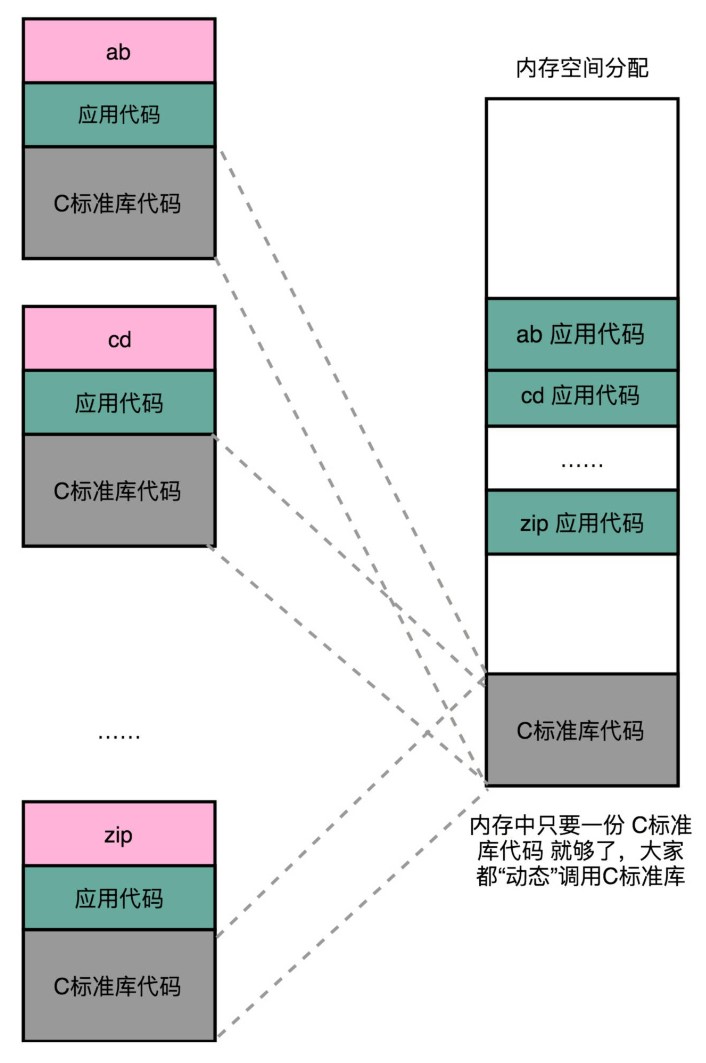
地址无关很重要，相对地址解烦恼

不过，要想要在程序运行的时候共享代码，也有一定的要求，就是这些机器码必须是“地址无关”的。也就是说，我们编译出来的共享库文件的指令代码，是地址无关码（Position-Independent Code）,就是地址不能写死，比如分支的跳转地址，函数的调用地址等，不能像静态链接的地址一样是个绝对的地址。换句话说就是，这段代码，无论加载在哪个内存地址，都能够正常执行。如果不是这样的代码，就是地址相关的代码。
你可以想想，大部分函数库其实都可以做到地址无关，因为它们都接受特定的输入，进行确定的操作，然后给出返回结果就好了。无论是实现一个向量加法，还是实现一个打印的函数，这些代码逻辑和输入的数据在内存里面的位置并不重要。
怎么样才能做到，动态共享库编译出来的代码指令，都是地址无关码呢？
动态代码库内部的变量和函数调用都很容易解决，我们只需要使用相对地址（Relative Address）就好了。各种指令中使用到的内存地址，给出的不是一个绝对的地址空间，而是一个相对于当前指令偏移量的内存地址。因为整个共享库是放在一段连续的虚拟内存地址中的，无论装载到哪一段地址，不同指令之间的相对地址都是不变的。

PLT 和 GOT，动态链接的解决方案

gcc lib.c -fPIC -shared -o lib.so

在编译的过程中，我们指定了一个 -fPIC 的参数。这个参数其实就是Position Independent Code 的意思，也就是我们要把这个编译成一个地址无关代码。

当调用一个动态库的函数时

call   400550 <show_me_the_money@plt>

这里后面有一个 @plt 的关键字，代表了我们需要从 PLT，也就是程序链接表（Procedure Link Table）里面找要调用的函数。对应的地址呢，则是 400550 这个地址。程序链接表是在编译期间就确定的了。
程序链接表里面放着动态库的地址，当动态库加载到本程序的虚拟地址空间后，就可以生成程序链接表中各个动态链接函数的地址了。
那当我们把目光挪到上面的 400550 这个地址，你又会看到里面进行了一次跳转，这个跳转指定的跳转地址，你可以在后面的注释里面可以看到，GLOBAL_OFFSET_TABLE+0x18。这里的 GLOBAL_OFFSET_TABLE，就是我接下来要说的全局偏移表。

  400550:       ff 25 12 05 20 00       jmp    QWORD PTR [rip+0x200512]        # 600a68 <_GLOBAL_OFFSET_TABLE_+0x18>

在动态链接对应的共享库，我们在共享库的 data section 里面，保存了一张全局偏移表（GOT，Global Offset Table）。虽然共享库的代码部分的物理内存是共享的，但是数据部分是各个动态链接它的应用程序里面各加载一份的。所有需要引用当前共享库外部的地址的指令，都会查询 GOT，来找到当前运行程序的虚拟内存里的对应位置。而 GOT 表里的数据，则是在我们加载一个个共享库的时候写进去的。

这样，虽然不同的程序调用的同样的动态库，各自的内存地址是独立的，调用的又都是同一个动态库，但是不需要去修改动态库里面的代码所使用的地址，而是各个程序各自维护好自己的 GOT，能够找到对应的动态库就好了。

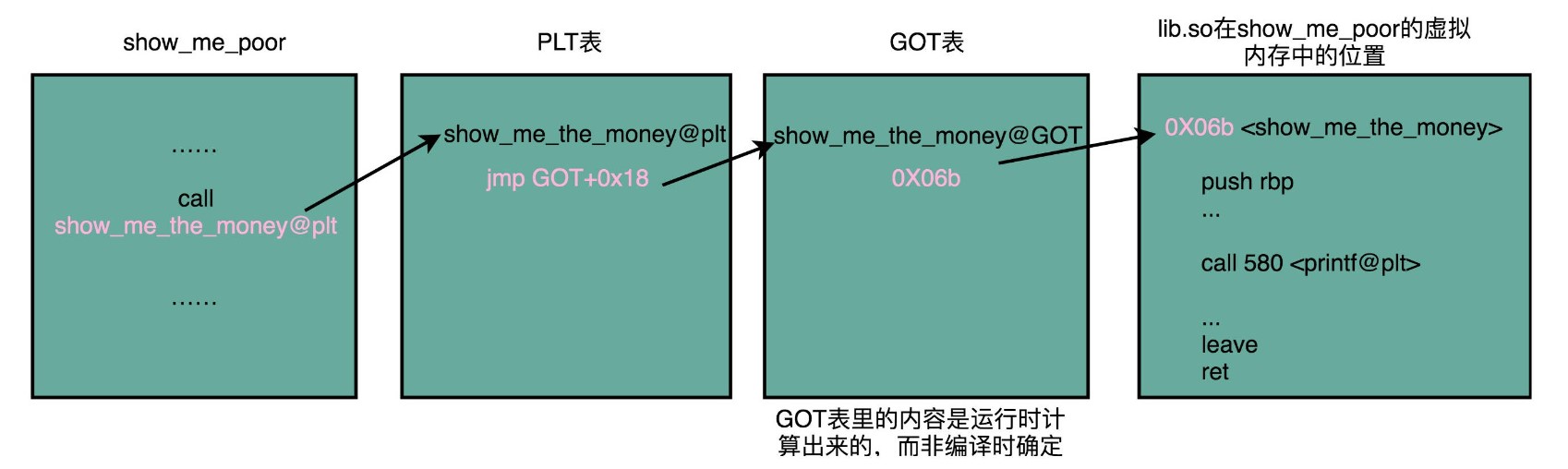
11 | 二进制编码：“手持两把锟斤拷，口中疾呼烫烫烫”？

数的表示


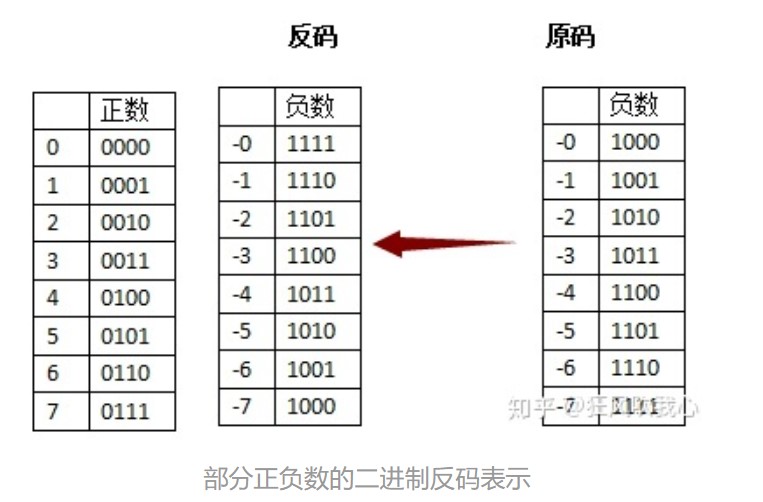
原码：是最简单的机器数表示法，用最高位表示符号位，其他位存放该数的二进制的绝对值。
反码：正数的反码还是等于原码；负数的反码就是它的原码除符号位外，按位取反。
补码：正数的补码等于它的原码；负数的补码等于反码+1

字符串的表示

[[c语言中文网-c教程笔记#ASCII编码，将英文存储到计算机]]
Unicode码

同样的文本，采用不同的编码存储下来。如果另外一个程序，用一种不同的编码方式来进行解码和展示，就会出现乱码。

“锟斤拷”的来源
如果我们想要用 Unicode 编码记录一些文本，特别是一些遗留的老字符集内的文本，但是这些字符在 Unicode 中可能并不存在。于是，Unicode 会统一把这些字符记录为 U+FFFD 这个编码。如果用 UTF-8 的格式存储下来，就是\xef\xbf\xbd。如果连续两个这样的字符放在一起，\xef\xbf\xbd\xef\xbf\xbd，这个时候，如果程序把这个字符，用 GB2312 的方式进行 decode，就会变成“锟斤拷”。

“烫烫烫”和“屯屯屯”的来源
如果你用了 Visual Studio 的调试器，默认使用 MBCS(多字节字符集)字符集。“烫”在里面是由 0xCCCC 来表示的，而 0xCC 又恰好是未初始化的内存的赋值。于是，在读到没有赋值的内存地址或者变量的时候，电脑就开始大叫“烫烫烫”了。
VC的DEBUG版会把未初始化的指针自动初始化为0xCCCCCCCC，而不是就让它随机去，那是因为DEBUG版的目的是为了方便我们调试程序的，如果野指针的初值不确定，那么每次调试同一个程序就可能出现不一样的结果，比如这次程序崩掉，下次正常运行，再一次虽然没崩掉，但结果不对……那显然对我们解bug是非常不利的。
DEBUG版本为了能让程序员更早的发现错误，把堆栈上的数据对初始化成了0xcc，也就是说局部变量如果不初始化，那么DEBUG版本中就会是0xCC
堆当中则会用0xCD来填充，也就是“屯屯屯屯屯”

12 | 理解电路：从电报机到门电路，我们如何做到“千里传信”？

与、或、非的电路都非常简单，要想做稍微复杂一点的工作，我们需要很多电路的组合。不过，这也彰显了现代计算机体系中一个重要的思想，就是通过分层和组合，逐步搭建起更加强大的功能。

可以说，电报是现代计算机的一个最简单的原型。它和我们现在使用的现代计算机有很多相似之处。我们通过电路的“开”和“关”，来表示“1”和“0”。就像晶体管在不同的情况下，表现为导电的“1”和绝缘的“0”的状态。

我们通过电报机这个设备，看到了如何通过“螺旋线圈 + 开关”，来构造基本的逻辑电路，我们也叫门电路。一方面，我们可以通过继电器或者中继，进行长距离的信号传输。另一方面，我们也可以通过设置不同的线路和开关状态，实现更多不同的信号表示和处理方式，这些线路的连接方式其实就是我们在数字电路中所说的门电路。而这些门电路，也是我们创建 CPU 和内存的基本逻辑单元。我们的各种对于计算机二进制的“0”和“1”的操作，其实就是来自于门电路，叫作组合逻辑电路。

13 | 加法器：如何像搭乐高一样搭电路（上）？


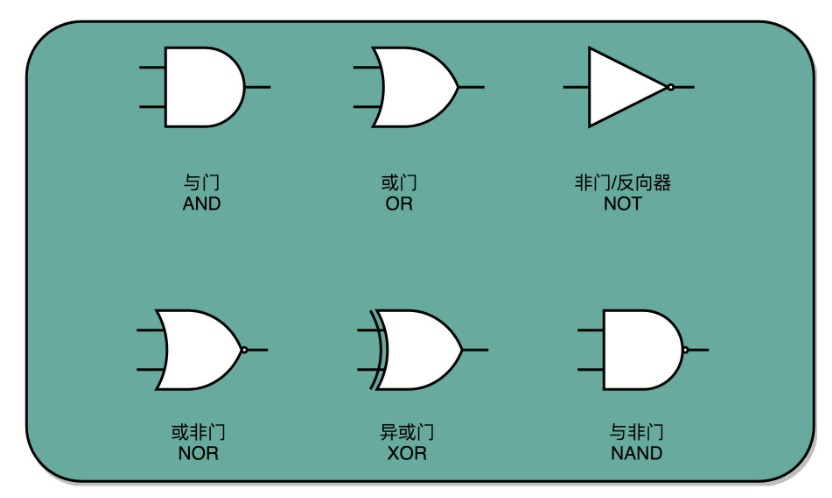
这些基本的门电路，是我们计算机硬件端的最基本的“积木”。我们今天包含十亿级别晶体管的现代 CPU，都是由这样一个一个的门电路组合而成的。

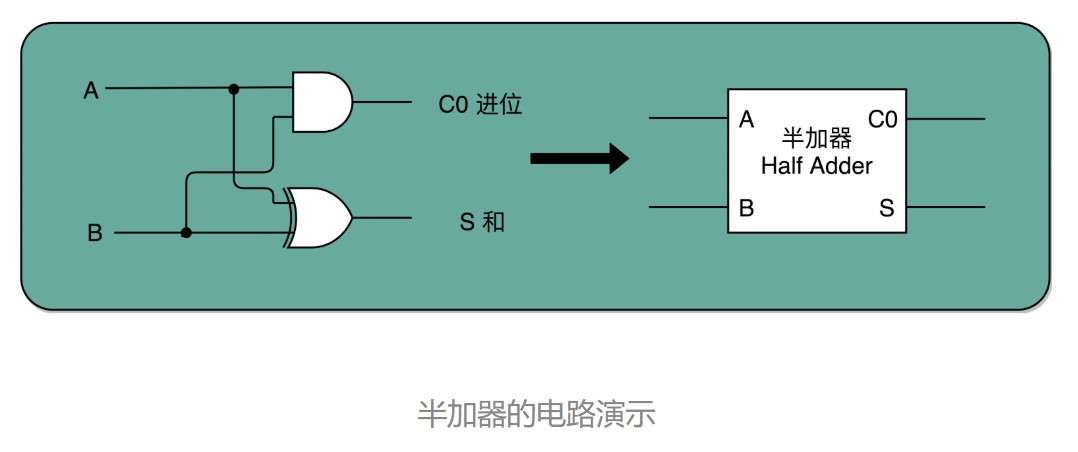
异或门和半加器

半加器：两个输入（加数1和加数2）和两个输出（进位和和）

二进制一位数加法

通过一个异或门计算出个位，通过一个与门计算出是否进位，我们就通过电路算出了一个一位数的加法。于是，我们把两个门电路打包，给它取一个名字，就叫作半加器（Half Adder），没有进位的输入。

全加器

全加器：三个输入（加数1、加数2和进位）和两个输出（进位和和）

我们用两个半加器和一个或门，就能组合成一个全加器。第一个半加器，我们用和个位的加法一样的方式，得到是否进位 X 和对应的二个数加和后的结果 Y，这样两个输出。然后，我们把这个加和后的结果 Y，和个位数相加后输出的进位信息 U，再连接到一个半加器上，就会再拿到一个是否进位的信号 V 和对应的加和后的结果 W。

有了全加器，我们要进行对应的两个 8 bit 数的加法就很容易了。我们只要把 8 个全加器串联起来就好了。

唯一需要注意的是，对于这个全加器，在个位，我们只需要用一个半加器，或者让全加器的进位输入始终是 0。因为个位没有来自更右侧的进位。而最左侧的一位输出的进位信号，表示的并不是再进一位，而是表示我们的加法是否溢出了。溢出位会存在条件寄存器中。

当我们想要搭建一个摩天大楼，我们需要很多很多楼梯。但是这个时候，我们已经不再关注最基础的一节楼梯是怎么用一块块积木搭建起来的。这其实就是计算机中，无论软件还是硬件中一个很重要的设计思想，分层。

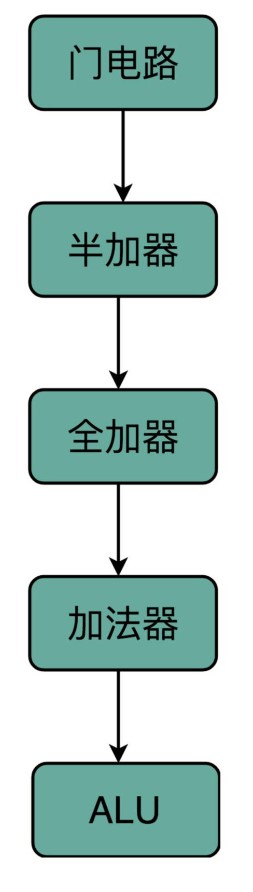
从简单到复杂，我们一层层搭出了拥有更强能力的功能组件。在上面的一层，我们只需要考虑怎么用下一层的组件搭建出自己的功能，而不需要下沉到更低层的其他组件然后弄清楚底层的实现原理。

在硬件层面，我们通过门电路、半加器、全加器一层层搭出了加法器这样的功能组件。我们把这些用来做算术逻辑计算的组件叫作 ALU，也就是算术逻辑单元。当进一步打造强大的 CPU 时，我们不会再去关注最细颗粒的门电路，只需要把门电路组合而成的 ALU，当成一个能够完成基础计算的黑盒子就可以了。

14 | 乘法器：如何像搭乐高一样搭电路（下）？

二进制乘法

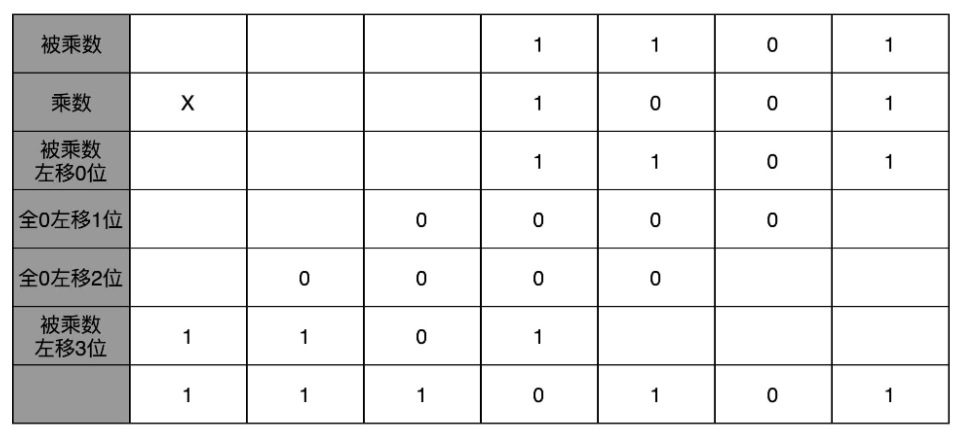
二进制的乘法优点是简单：实际的乘法，就退化成了位移和加法。

乘法器运算的步骤
先拿乘数最右侧的个位乘以被乘数，然后把结果写入用来存放计算结果的开关里面，然后，把被乘数左移一位（相当于乘2），把乘数右移一位(目的是使乘数的个位数为其操作对象)，仍然用乘数个位去乘以被乘数，然后把结果加到刚才的结果上。反复重复这一步骤，直到不能再左移和右移位置。这样，乘数和被乘数就像两列相向而驶的列车，仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路，就能完成整个乘法。
这个计算方式虽然节约电路了，但是也有一个很大的缺点，那就是慢。
你应该很容易就能发现，在这个乘法器的实现过程里，我们其实就是把乘法展开，变成了“加法 + 位移”来实现。我们用的是 4 位数，所以要进行 4 组“位移 + 加法”的操作。而且这 4 组操作还不能同时进行。因为下一组的加法要依赖上一组的加法后的计算结果，下一组的位移也要依赖上一组的位移的结果。这样，整个算法是“顺序”的，每一组加法或者位移的运算都需要一定的时间，跟位数乘正比。

并行加速方法

那么，我们有没有办法，把时间复杂度上降下来呢？研究数据结构和算法的时候，我们总是希望能够把 O(N) 的时间复杂度，降低到 O(logN)。办法还真的有。和软件开发里面改算法一样，在涉及 CPU 和电路的时候，我们可以改电路。

分而治之，但是会产生很多中间结果。

电路并行

上面我们说的并行加速的办法，看起来还是有点儿笨。我们回头来做一个抽象的思考。之所以我们的计算会慢，核心原因其实是“顺序”计算，也就是说，需要等前面的计算结果完成之后，我们才能得到后面的计算结果。
最典型的例子就是我们上一讲讲的加法器。每一个全加器，都要等待上一个全加器，把对应的进入输入结果算出来，才能算下一位的输出。位数越多，越往高位走，等待前面的步骤就越多，这个等待的时间有个专门的名词，叫作门延迟（Gate Delay）。
每通过一个门电路，我们就要等待门电路的计算结果，就是一层的门电路延迟，我们一般给它取一个“T”作为符号。一个全加器，其实就已经有了 3T 的延迟（进位需要经过 3 个门电路）。而 4 位整数，最高位的计算需要等待前面三个全加器的进位结果，也就是要等 9T 的延迟。如果是 64 位整数，那就要变成 63×3=189T 的延迟。这可不是个小数字啊！
除了门延迟之外，还有一个问题就是时钟频率。在上面的顺序乘法计算里面，如果我们想要用更少的电路，计算的中间结果需要保存在寄存器里面，然后等待下一个时钟周期的到来，控制测试信号才能进行下一次移位和加法，这个延迟比上面的门延迟更可观。
那怎么才能把线路连结得复杂一点，让高位和低位的计算同时出结果呢？怎样才能让高位不需要等待低位的进位结果，而是把低位的所有输入信号都放进来，直接计算出高位的计算结果和进位结果呢？
我们只要把进位部分的电路完全展开就好了。我们的半加器到全加器，再到加法器，都是用最基础的门电路组合而成的。门电路的计算逻辑，可以像我们做数学里面的多项式乘法一样完全展开。在展开之后呢，我们可以把原来需要较少的，但是有较多层前后计算依赖关系的门电路，展开成需要较多的，但是依赖关系更少的门电路。
下面的示意图，展示了一下我们加法器。如果我们完全展开电路，高位的进位和计算结果，可以和低位的计算结果同时获得。这个的核心原因是电路是天然并行的，一个输入信号，可以同时传播到所有接通的线路当中。

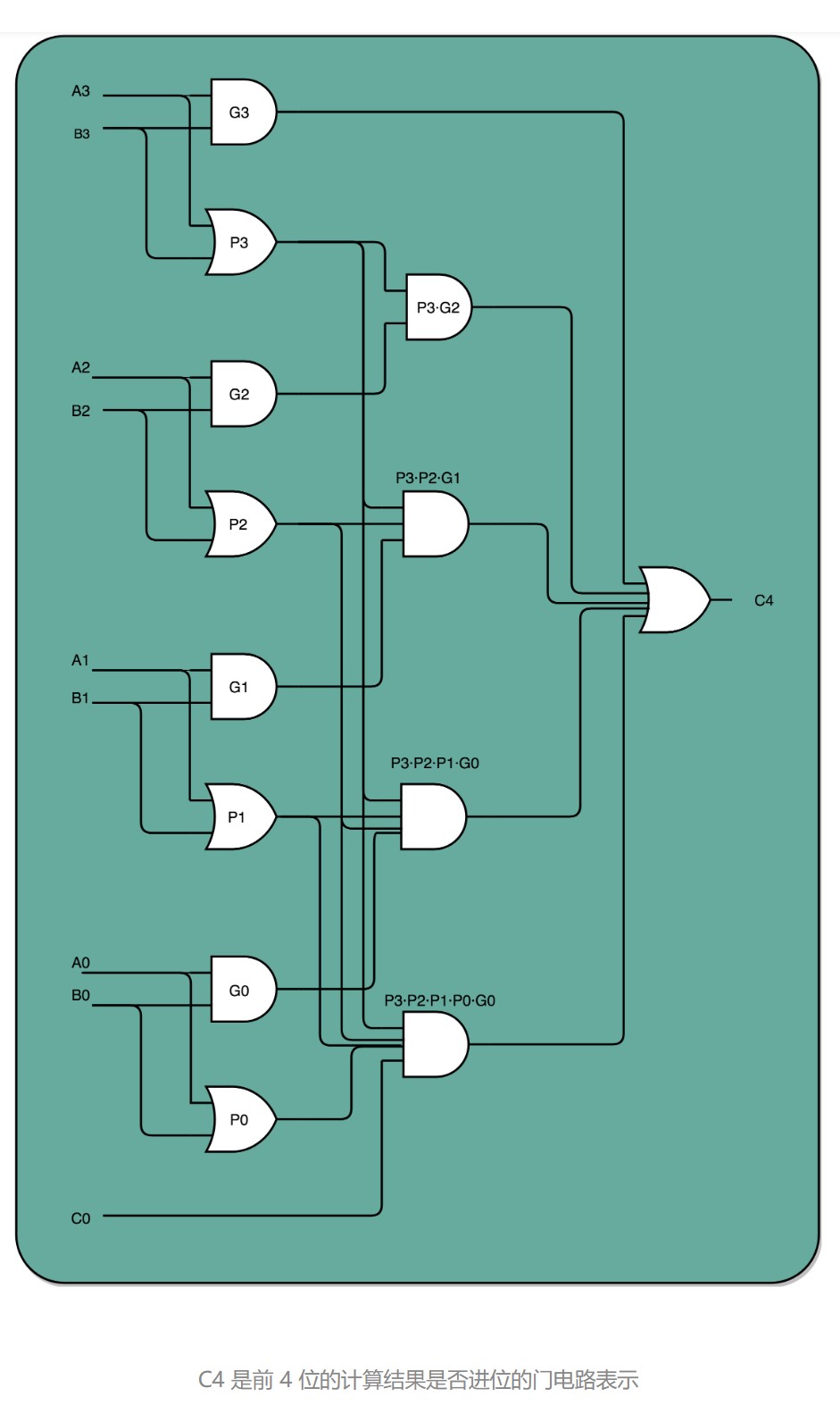
如果一个 4 位整数最高位是否进位，展开门电路图，你会发现，我们只需要 3T 的延迟就可以拿到是否进位的计算结果。而对于 64 位的整数，也不会增加门延迟，只是从上往下复制这个电路，接入更多的信号而已。看到没？我们通过把电路变复杂，就解决了延迟的问题。
这个优化，本质上是利用了电路天然的并行性。电路只要接通，输入的信号自动传播到了所有接通的线路里面，这其实也是硬件和软件最大的不同。
无论是这里把对应的门电路逻辑进行完全展开以减少门延迟，还是上面的乘法通过并行计算多个位的乘法，都是把我们完成一个计算的电路变复杂了。而电路变复杂了，也就意味着晶体管变多了。

之前很多同学在我们讨论计算机的性能问题的时候，都提到，为什么晶体管的数量增加可以优化计算机的计算性能。实际上，这里的门电路展开和上面的并行计算乘法都是很好的例子。我们通过更多的晶体管，就可以拿到更低的门延迟，以及用更少的时钟周期完成一个计算指令。

总结延伸

讲到这里，相信你已经发现，我们通过之前两讲的 ALU 和门电路，搭建出来了乘法器。如果愿意的话，我们可以把很多在生活中不得不顺序执行的事情，通过简单地连结一下线路，就变成并行执行了。这是因为，硬件电路有一个很大的特点，那就是信号都是实时传输的。

我们也看到了，通过精巧地设计电路，用较少的门电路和寄存器，就能够计算完成乘法这样相对复杂的运算。
是用更少更简单的电路，但是需要更长的门延迟和时钟周期；还是用更复杂的电路，但是更短的门延迟和时钟周期来计算一个复杂的指令，这之间的权衡，其实就是计算机体系结构中 RISC 和 CISC 的经典历史路线之争。

15 | 浮点数和定点数（上）：怎么用有限的Bit表示尽可能多的信息？

我们用 32 个比特，能够表示所有实数吗？
答案很显然是不能。32 个比特，只能表示 2 的 32 次方个不同的数，差不多是 40 亿个。根本原因在于计算机表示的数是离散的，用离散的量表示连续的实数的量只能近似的模拟，而不能所有的完全表示。

40 亿个数看似已经很多了，但是比起无限多的实数集合却只是沧海一粟。所以，这个时候，计算机的设计者们，就要面临一个问题了：我到底应该让这 40 亿个数映射到实数集合上的哪些数，在实际应用中才能最划得来呢？

定点数的表示

用 4 个比特来表示 0～9 的整数，那么 32 个比特就可以表示 8 个这样的整数。然后我们把最右边的 2 个 0～9 的整数，当成小数部分；把左边 6 个 0～9 的整数，当成整数部分。这样，我们就可以用 32 个比特，来表示从 0 到 999999.99 这样 1 亿个实数了。
这种用二进制来表示十进制小数的编码方式，叫作BCD编码（Binary-Coded Decimal）。

缺点是：表示的范围太小，没办法同时表示很大的数字和很小的数字

浮点数的表示

在计算机里，可以用科学计数法来表示实数。浮点数的科学计数法的表示，有一个IEEE的标准，它定义了两个基本的格式。一个是用 32 比特表示单精度的浮点数，也就是我们常常说的 float 或者 float32 类型。另外一个是用 64 比特表示双精度的浮点数，也就是我们平时说的 double 或者 float64 类型。

单精度的 32 个比特可以分成三部分。

第一部分是一个符号位，用来表示是正数还是负数。我们一般用s来表示。在浮点数里，我们不像正数分符号数还是无符号数，所有的浮点数都是有符号的。

接下来是一个 8 个比特组成的指数位。我们一般用e来表示。8 个比特能够表示的整数空间，就是 0～255。我们在这里用 1～254 映射到 -126～127 这 254 个有正有负的数上。因为我们的浮点数，不仅仅想要表示很大的数，还希望能够表示很小的数，所以指数位也会有负数。

你发现没，我们没有用到 0 和 255。没错，这里的 0（也就是 8 个比特全部为 0） 和 255 （也就是 8 个比特全部为 1）另有它用。

最后，是一个 23 个比特组成的有效数位。我们用f来表示。综合科学计数法，我们的浮点数就可以表示成下面这样：

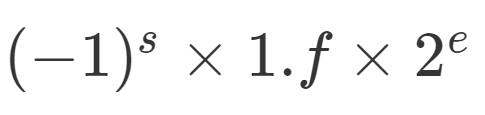
16 | 浮点数和定点数（下）：深入理解浮点数到底有什么用？

浮点数的二进制转化

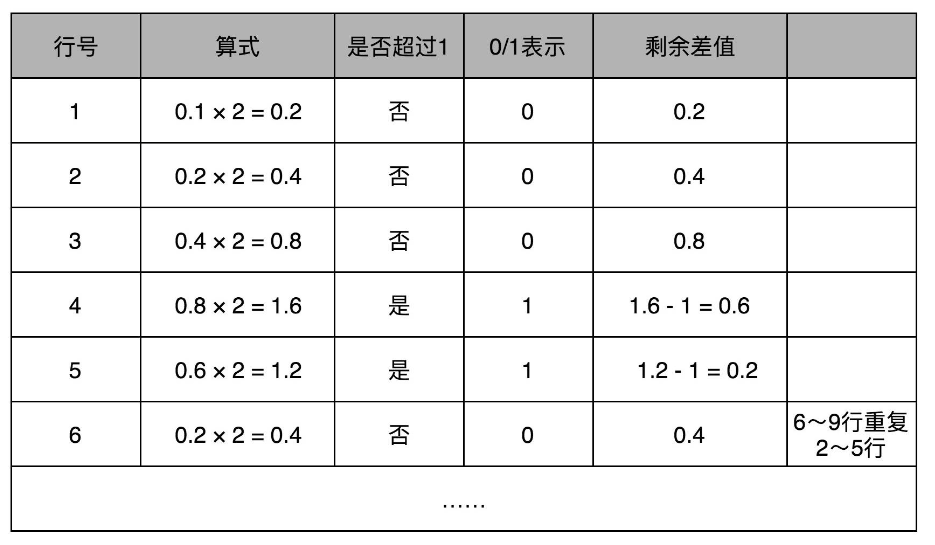
和整数的二进制表示采用“除以 2，然后看余数”的方式相比，小数部分转换成二进制是用一个相似的反方向操作，就是乘以 2，然后看看是否超过 1。如果超过 1，我们就记下 1，并把结果减去 1，进一步循环操作。

例：0.1的二进制表示

例：十进制0.5用二进制表示为0.1，相当于二分之一

浮点数的加法和精度损失

搞清楚了怎么把一个十进制的数值，转化成 IEEE-754 标准下的浮点数表示，我们现在来看一看浮点数的加法是怎么进行的。其实原理也很简单，你记住六个字就行了，那就是先对齐、再计算。
两个浮点数的指数位可能是不一样的，所以我们要把两个的指数位，变成一样的，然后只去计算有效位的加法就好了。
比如 0.5，表示成浮点数，对应的指数位是 -1，有效位是 00…（后面全是 0，记住 f 前默认有一个 1）。0.125 表示成浮点数，对应的指数位是 -3，有效位也还是 00…（后面全是 0，记住 f 前默认有一个 1）。

那我们在计算 0.5+0.125 的浮点数运算的时候，首先要把两个的指数位对齐，也就是把指数位都统一成两个其中较大的 -1。对应的有效位 1.00…也要对应右移两位，因为 f 前面有一个默认的 1，所以就会变成 0.01。然后我们计算两者相加的有效位 1.f，就变成了有效位 1.01，而指数位是 -1，这样就得到了我们想要的加法后的结果。
实现这样一个加法，也只需要位移。和整数加法类似的半加器和全加器的方法就能够实现，在电路层面，也并没有引入太多新的复杂性。
回到浮点数的加法过程，你会发现，其中指数位较小的数，需要在有效位进行右移，在右移的过程中，最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。两个相加数的指数位差的越大，位移的位数越大，可能丢失的精度也就越大。

32 位浮点数的有效位长度一共只有 23 位，如果两个数的指数位差出 23 位，较小的数右移 24 位之后，所有的有效位就都丢失了。这也就意味着，虽然浮点数可以表示上到 3.40×10^38 下到 1.17×10^−38 这样的数值范围。但是在实际计算的时候，只要两个数，差出 2^24，也就是差不多 1600 万倍，那这两个数相加之后，结果完全不会变化。

Kahan Summation 算法

一个常见的应用场景是，在一些“积少成多”的计算过程中，比如在机器学习中，我们经常要计算海量样本计算出来的梯度或者 loss，于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大，但是随着累积值的越来越大，就会出现“大数吃小数”的情况。

public class FloatPrecision {
  public static void main(String[] args) {
    float sum = 0.0f;
    for (int i = 0; i < 20000000; i++) {
        float x = 1.0f;
        sum += x;
    }
    // 加到 1600 万之后的加法因为精度丢失都没有了
    System.out.println("sum is " + sum);
  }
}

聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作Kahan Summation的算法来解决这个问题

public class KahanSummation {
  public static void main(String[] args) {
    float sum = 0.0f;
    float c = 0.0f;
    for (int i = 0; i < 20000000; i++) {
        float x = 1.0f;
        float y = x - c;
        float t = sum + y;
        c = (t-sum)-y;
        sum = t;
    }
    System.out.println("sum is " + sum);
  }
}

其实这个算法的原理其实并不复杂，就是在每次的计算过程中，都用一次减法，把当前加法计算中损失的精度记录下来，然后在后面的循环中，把这个精度损失放在要加的小数上，再做一次运算。

总结延伸

到这里，我们已经讲完了浮点数的表示、加法计算以及可能会遇到的精度损失问题。可以看到，虽然浮点数能够表示的数据范围变大了很多，但是在实际应用的时候，由于存在精度损失，会导致加法的结果和我们的预期不同，乃至于完全没有加上的情况。

所以，一般情况下，在实践应用中，对于需要精确数值的，比如银行存款、电商交易，我们都会使用定点数或者整数类型。
比方说，你一定在 MySQL 里用过 decimal(12,2)，来表示订单金额。如果我们的银行存款用 32 位浮点数表示，就会出现，马云的账户里有 2 千万，我的账户里只剩 1 块钱。结果银行一汇总总金额，那 1 块钱在账上就“不翼而飞”了。