 忧郁的大能猫
忧郁的大能猫
好奇的探索者,理性的思考者,踏实的行动者。
blog/A-IT/50-应用方向/机器学习/书籍/深度学习入门:基于Python的理论与实现
Table of Contents:
本书最大的特点是“剖解”了深度学习的底层技术。正如美国物理学家理查德·费曼(Richard Phillips Feynman)所说: “What I cannot create, I do not understand.”只有创造一个东西,才算真正弄懂了一个问题。
第1章 Python入门
第2章 感知机
感知机是什么
• 感知机是具有输入和输出的算法。给定一个输入后,将输出一个既定的值。可以作为神经网络的神经元
• 感知机将权重和偏置设定为参数。
• 使用感知机可以表示与门和或门等逻辑电路。
• 异或门无法通过单层感知机来表示。
• 使用2层感知机可以表示异或门。
• 单层感知机只能表示线性空间,而多层感知机可以表示非线性空间。
• 多层感知机(在理论上)可以表示计算机。
感知机的图的表示
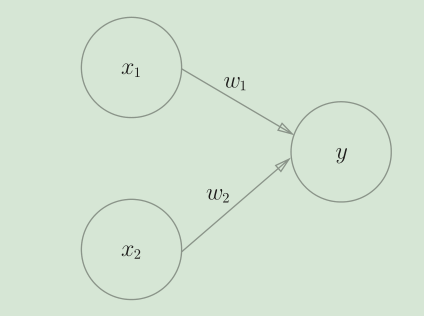
感知机的公式
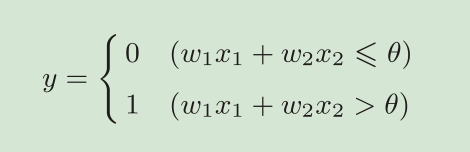
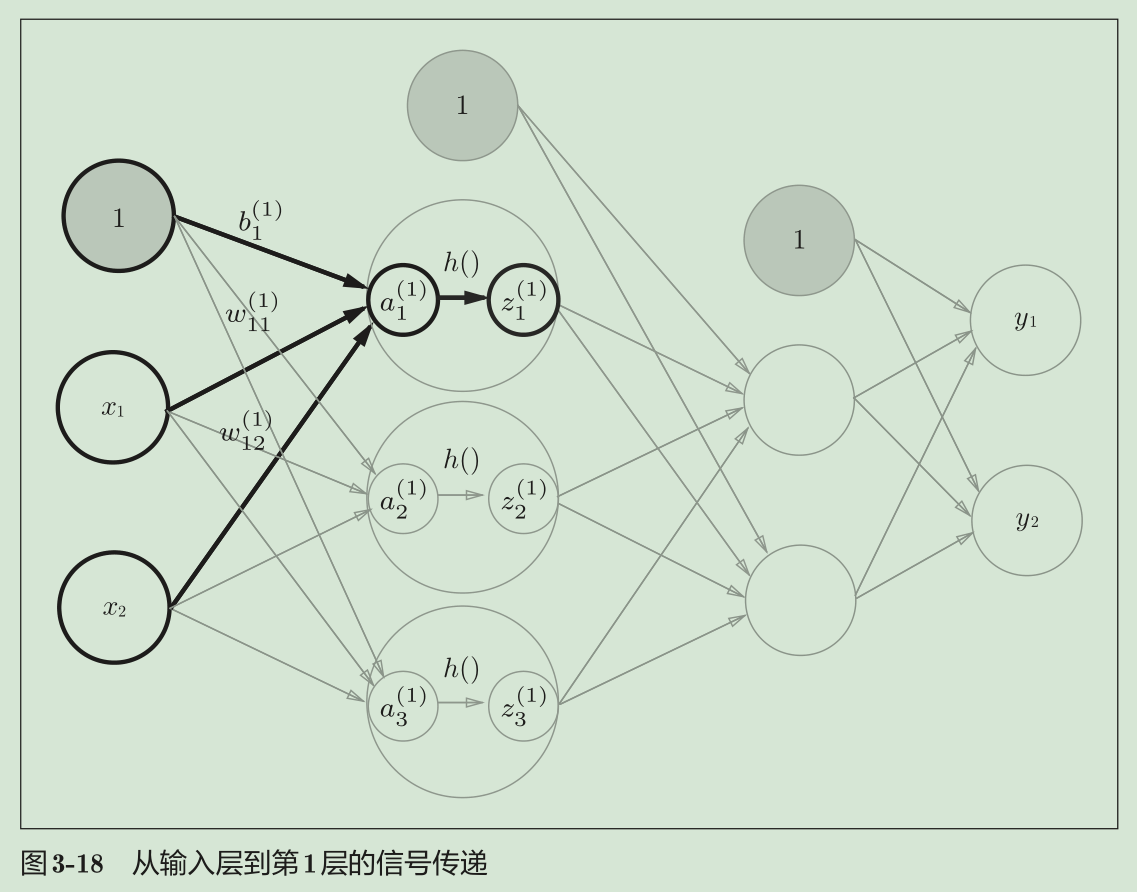
神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活” 。这里将这个界限值称为阈值,用符号θ表示。 阈值可以移到不等式的左边,−θ命名为偏置b
使用函数表示感知机
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y多层感知机
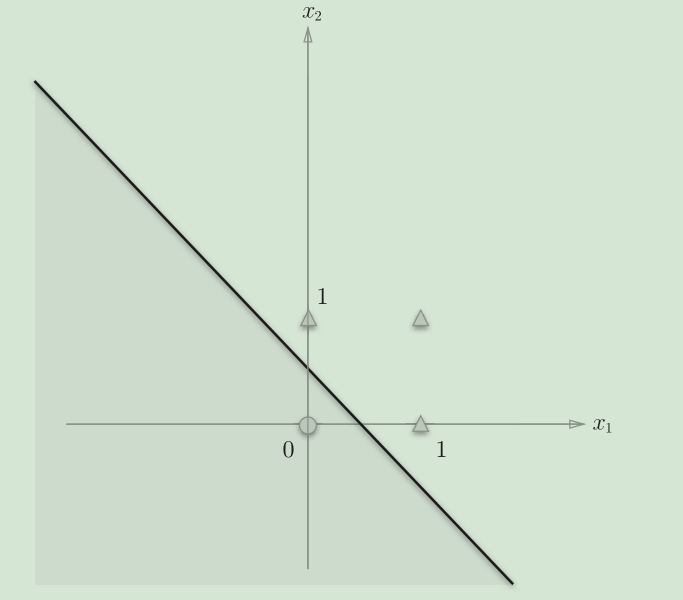
OR的图,分割线是一个线性函数
XOR的图,分割线是多个进行分割
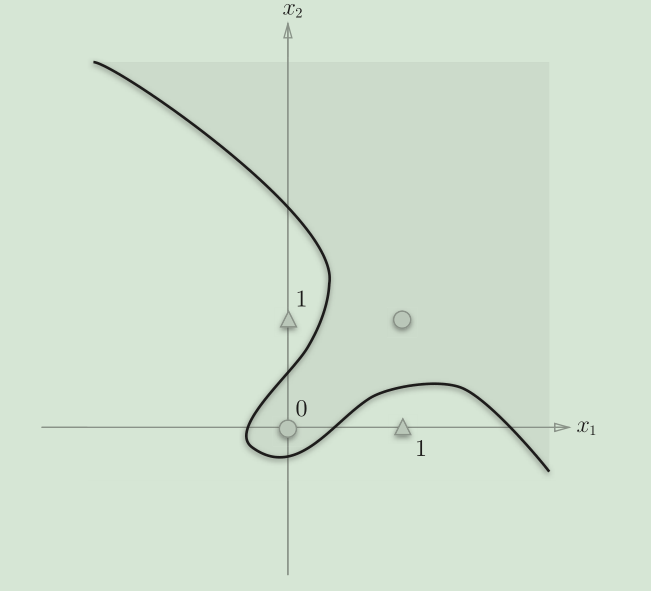
上图中中的○和△无法用一条直线分开,但是如果将“直线”这个限制条件去掉,就可以实现了。
感知机的局限性就在于它只能表示由一条直线分割的空间。上图这样弯曲的曲线无法用感知机表示。另外,上图这样的曲线分割而成的空间称为非线性空间,由直线分割而成的空间称为线性空间
感知机不能表示异或门让人深感遗憾,但也无需悲观。实际上,感知机的绝妙之处在于它可以“叠加层”
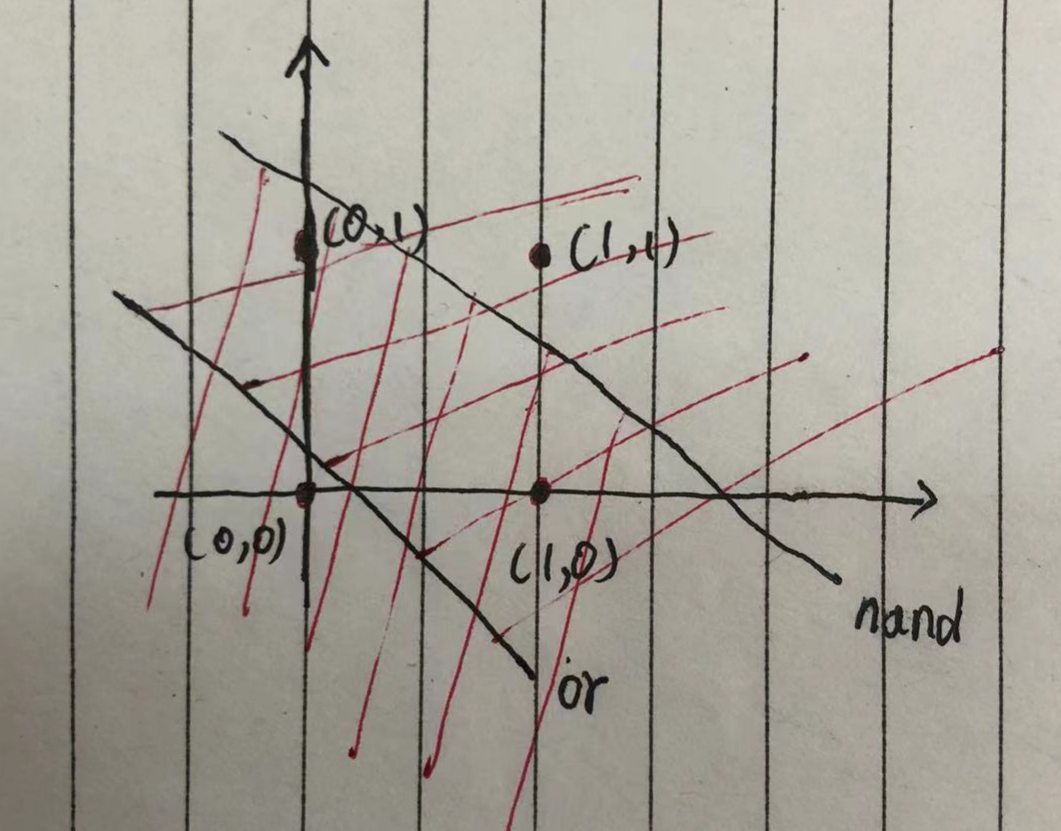
上图表示的含义为:先求出NAND为1的区域,再求出OR的区域,两者重叠(AND)的区域便是XOR的区域。
因为没有用非线性的sigmoid函数的感知机,所以上面的区域依然是线性围起来的空间
实际上,与门、或门是单层感知机,而异或门是2层感知机。叠加了多层的感知机也称为多层感知机(multi-layered perceptron)。
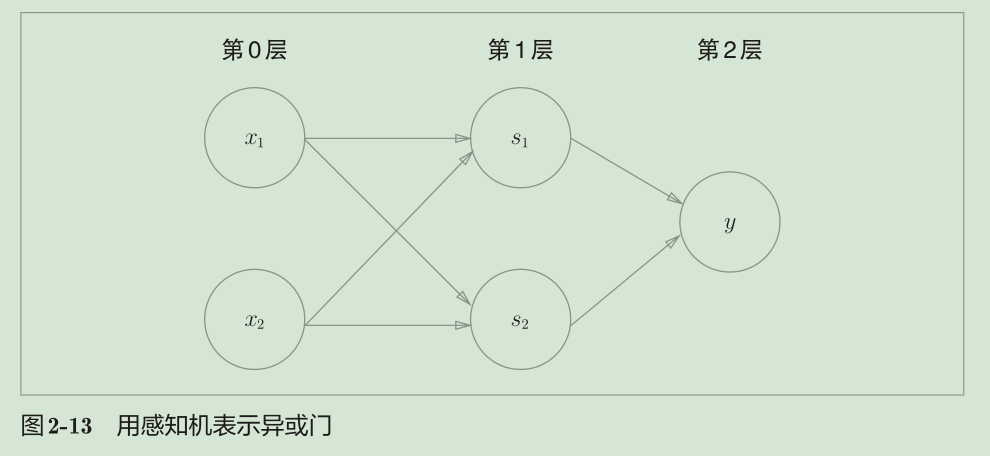
s1相当于NAND,s2相当于OR,y相当于AND
理论上可以说2层感知机就能构建计算机。这是因为,已有研究证明,2层感知机可以表示任意函数。但是,使用2层感知机的构造,通过设定合适的权重来构建计算机是一件非常累人的事情。实际上,在用与非门等低层的元件构建计算机的情况下,分阶段地制作所需的零件(模块)会比较自然,即先实现与门和或门,然后实现半加器和全加器,接着实现算数逻辑单元(ALU),然后实现CPU。因此,通过感知机表示计算机时,使用叠加了多层的构造来实现是比较自然的流程。
第3章 神经网络
• 神经网络中的激活函数使用平滑变化的 sigmoid 函数或 ReLU 函数。
• 通过巧妙地使用NumPy多维数组,可以高效地实现神经网络。
• 机器学习的问题大体上可以分为回归问题和分类问题。
• 关于输出层的激活函数,回归问题中一般用恒等函数,分类问题中一般用softmax函数。
• 分类问题中,输出层的神经元的数量设置为要分类的类别数。
• 输入数据的集合称为批。通过以批为单位进行推理处理,能够实现高速的运算。
从感知机到神经网络
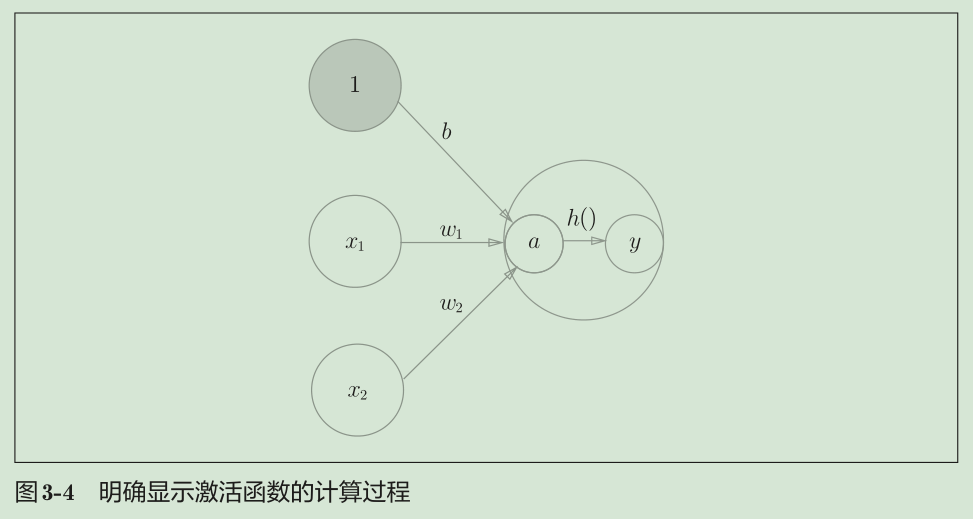
区别在于激活函数的不同
可以说感知机中使用了阶跃函数作为激活函数, 在激活函数的众多候选函数中,感知机使用了阶跃函数
而神经网络则使用其他的激活函数
激活函数
阶跃函数的实现
def step_function(x):
if x > 0:
return 1
else:
return 0
# 改为支持NumPy数组
def step_function(x):
y = x > 0
return y.astype(np.int64)
def step_function(x):
return np.array(x > 0, dtype=np.int64)sigmoid函数的实现
def sigmoid(x):
return 1 / (1 + np.exp(-x))ReLU函数(Rectified Linear Unit)
def relu(x):
return np.maximum(0, x)非线性函数
函数本来是输入某个值后会返回一个值的转换器。向这个转换器输入某个值后,输出值是输入值的常数倍的函数称为线性函数(用数学式表示为h(x) = cx。c为常数)。因此,线性函数是一条笔直的直线。而非线性函数,顾名思义,指的是不像线性函数那样呈现出一条直线的函数。
阶跃函数和sigmoid函数还有其他共同点,就是两者均为非线性函数。sigmoid函数是一条曲线,阶跃函数是一条像阶梯一样的折线,两者都属于非线性的函数
神经网络的激活函数必须使用非线性函数。换句话说,激活函数不能使用线性函数。为什么不能使用线性函数呢?因为使用线性函数的话,加深神经网络的层数就没有意义了。
线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。为了具体地(稍微直观地)理解这一点,我们来思考下面这个简单的例子。这里我们考虑把线性函数h(x) = cx作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络 。这个运算会进行y(x) = c × c × c × x的乘法运算,但是同样的处理可以由y(x) = ax(注意,a = c3 )这一次乘法运算(即没有隐藏层的神经网络)来表示。如本例所示,使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所带来的优势,激活函数必须使用非线性函数。
3层神经网络的实现
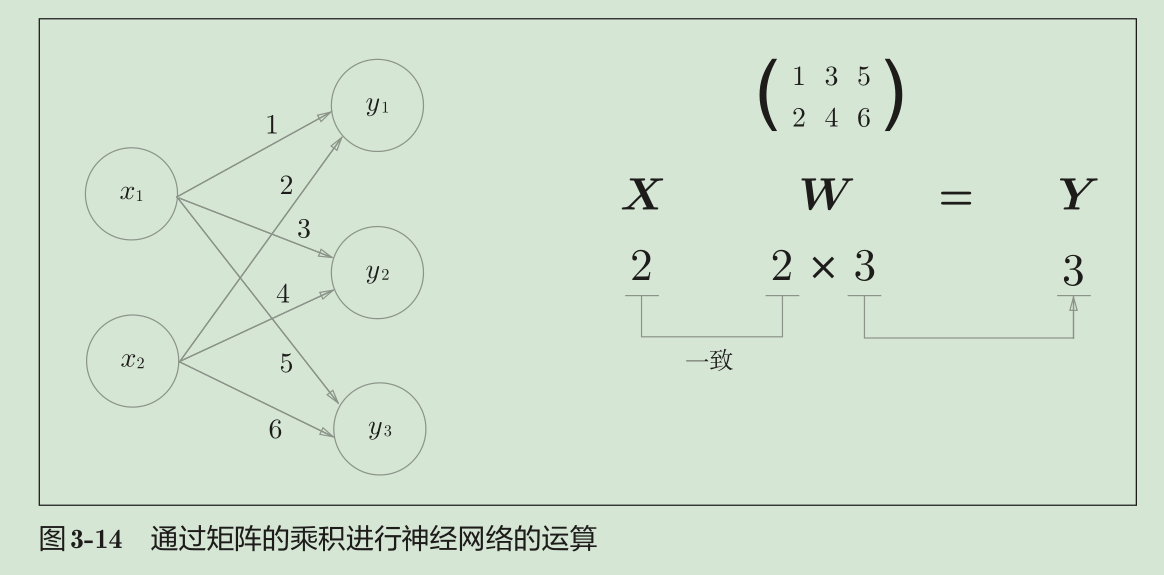
代码实现
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]输出层的设计
机器学习的问题大致可以分为分类问题和回归问题。
分类问题是数据属于哪一个类别的问题。比如,区分图像中的人是男性还是女性的问题就是分类问题。
回归问题是根据某个输入预测一个(连续的)数值的问题。比如,根据一个人的图像预测这个人的体重的问题就是回归问题(类似“57.4kg”这样的预测)。
一般而言,回归问题用恒等函数,分类问题用softmax函数。
恒等函数
恒等函数会将输入按原样输出,对于输入的信息,不加以任何改动地直接输出
softmax函数
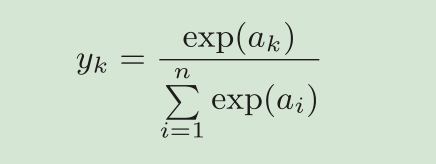
exp(x)是表示e x 的指数函数(e是纳皮尔常数2.7182 ... )。表示假设输出层共有n个神经元,计算第k个神经元的输出y k 。如式所示,softmax函数的分子是输入信号ak 的指数函数,分母是所有输入信号的指数函数的和。
实现softmax函数时的注意事项
softmax函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大,从而造成溢出问题。
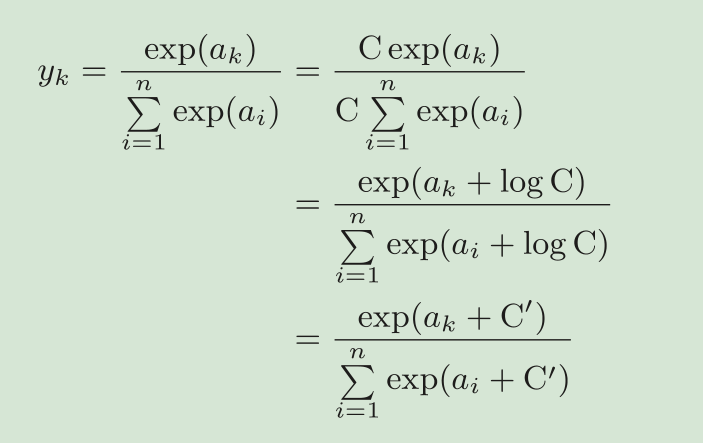
上式说明,在进行softmax的指数函数的运算时,加上(或者减去)某个常数并不会改变运算的结果。这里的C可以使用任何值,但是为了防止溢出,一般会使用输入信号中的最大值。
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(a)
>>> print(y)
[ 0.01821127 0.24519181 0.73659691]
>>> np.sum(y)
1.0softmax函数的特征
softmax函数的输出是0.0到1.0之间的实数。并且,softmax函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正因为有了这个性质,我们才可以把softmax函数的输出解释为“概率”。
这里需要注意的是,即便使用了softmax函数,各个元素之间的大小关系也不会改变。这是因为指数函数(y = exp(x))是单调递增函数。实际上,上例中 a 的各元素的大小关系和 y 的各元素的大小关系并没有改变。
推理阶段一般会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关系
输出层的神经元数量
输出层的神经元数量需要根据待解决的问题来决定。
对于分类问题,输出层的神经元数量一般设定为类别的数量。比如,对于某个输入图像,预测是图中的数字0到9中的哪一个的问题(10类别分类问题),可以像图3-23这样,将输出层的神经元设定为10个。
手写数字识别
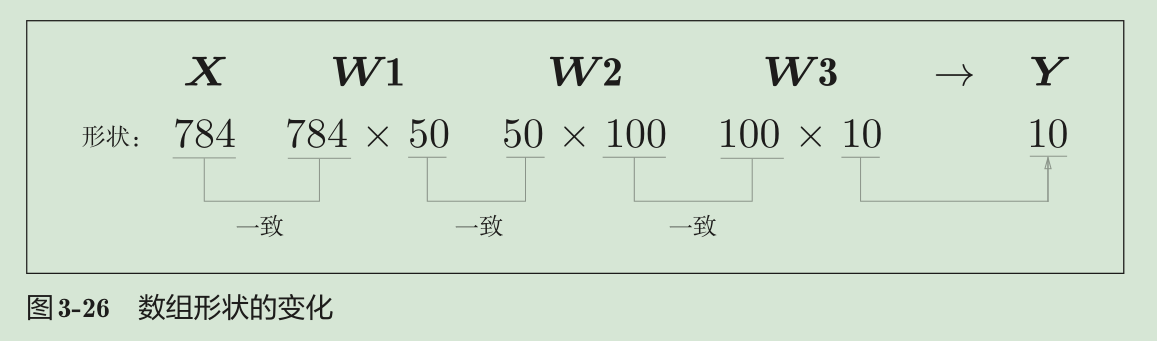
输入一个由784个元素(原本是一个28 × 28的二维数组)构成的一维数组后,输出一个有10个元素的一维数组。这是只输入一张图像数据时的处理流程。
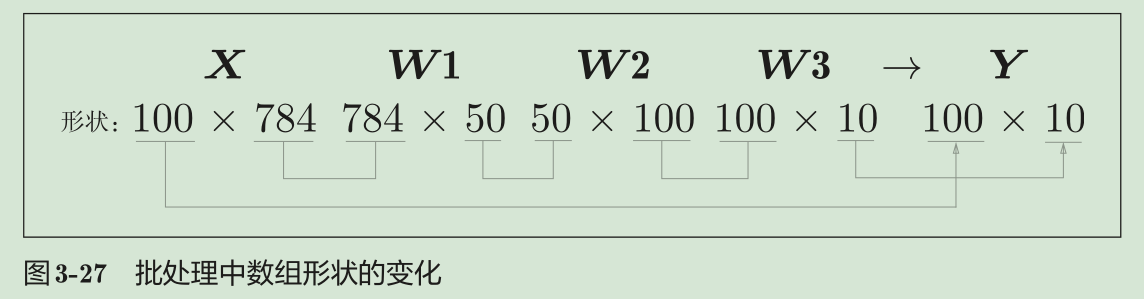
批处理:输入数据的形状为100 × 784,输出数据的形状为100 × 10。这表示输入的100张图像的结果被一次性输出了
第4章 神经网络的学习
本章介绍了神经网络的学习。首先,为了能顺利进行神经网络的学习,我们导入了损失函数这个指标。以这个损失函数为基准,找出使它的值达到最小的权重参数,就是神经网络学习的目标。为了找到尽可能小的损失函数值,我们介绍了使用函数斜率的梯度法。
• 机器学习中使用的数据集分为训练数据和测试数据。
• 神经网络用训练数据进行学习,并用测试数据评价学习到的模型的泛化能力。
• 神经网络的学习以损失函数为指标,更新权重参数,以使损失函数的值减小。
• 利用某个给定的微小值的差分求导数的过程,称为数值微分。
• 利用数值微分,可以计算权重参数的梯度。
• 数值微分虽然费时间,但是实现起来很简单。下一章中要实现的稍微复杂一些的误差反向传播法可以高速地计算梯度。
从数据中学习
先从图像中提取特征量,再用机器学习技术学习这些特征量的模式。这里所说的“特征量”是指可以从输入数据(输入图像)中准确地提取本质数据(重要的数据)的转换器。图像的特征量通常表示为向量的形式。在计算机视觉领域,常用的特征量包括SIFT、SURF和HOG等。使用这些特征量将图像数据转换为向量,然后对转换后的向量使用机器学习中的SVM、KNN等分类器进行学习。
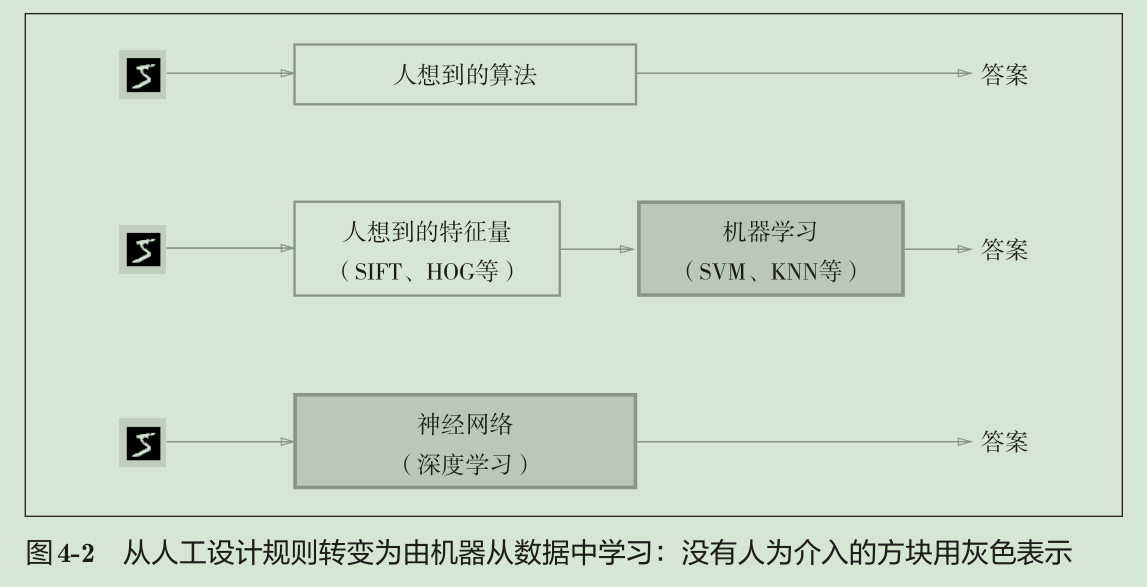
神经网络的优点是对所有的问题都可以用同样的流程来解决。比如,不管要求解的问题是识别5,还是识别狗,抑或是识别人脸,神经网络都是通过不断地学习所提供的数据,尝试发现待求解的问题的模式。
损失函数
损失函数是表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。
均方误差(mean squared error)
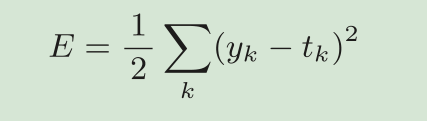
代码实现:
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
>>> # 设“2”为正确解
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>>
>>> # 例1:“2”的概率最高的情况(0.6)
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.097500000000000031交叉熵误差(cross entropy error)
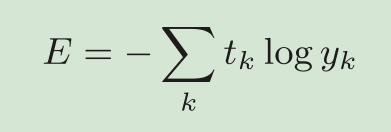

代码实现:
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
0.51082545709933802函数内部在计算 np.log 时,加上了一个微小值 delta 。这是因为,当出现 np.log(0) 时, np.log(0) 会变为负无限大的 -inf ,这样一来就会导致后续计算无法进行。作为保护性对策,添加一个微小值可以防止负无限大的发生。
mini-batch学习
神经网络的学习也是从训练数据中选出一批数据(称为mini-batch,小批量),然后对每个mini-batch进行学习。比如,从60000个训练数据中随机选择100笔,再用这100笔数据进行学习。这种学习方式称为mini-batch学习
mini-batch版交叉熵误差的实现
# one-hot版
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size # 除batch_size是为了进行正规化
# 非one-hot版
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size为何要设定损失函数
在进行神经网络的学习时,不能将识别精度作为指标。因为如果以识别精度为指标,则参数的导数在绝大多数地方都会变为0
识别精度(或准确率)通常被定义为分类正确的样本数量与总样本数量的比值。这个比率是一个离散的值。
识别精度是基于离散的分类结果计算得出的,而且即使微小的参数变化也可能不会立即改变分类结果。举例来说,如果你的模型在100笔数据中正确识别了32笔,识别精度为32%。微调参数可能不会立即影响分类结果,因此识别精度会保持在32%。即使有所改善,也可能会从32%跳跃到33%或34%,而不是以连续的方式变化。
相比之下,当使用损失函数作为指标时,通常是连续的。损失函数是一个连续的函数,它对参数的微小变化会产生相应的连续变化。如果稍微改变参数,损失函数值可能会从0.92543连续地变化到0.93432等。
识别精度对微小的参数变化基本上没有什么反应,即便有反应,它的值也是不连续地、突然地变化。作为激活函数的阶跃函数也有同样的情况。出于相同的原因,如果使用阶跃函数作为激活函数,神经网络的学习将无法进行。
阶跃函数的导数在绝大多数地方(除了0以外的地方)均为0。就是说,如果使用了阶跃函数,那么即便将损失函数作为指标,参数的微小变化也会被阶跃函数抹杀,导致损失函数的值不会产生任何变化。
数值微分
代码实现:
# 不好的实现示例
def numerical_diff_0(f, x):
h = 10e-50
return (f(x+h) - f(x)) / h
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)函数 numerical_diff(f, x) 的名称来源于数值微分的英文numerical differentiation
numerical_diff_0有两个问题:
1. h 使用了 10e-50 这个微小值。但是,这样反而产生了舍入误差(rounding error)。
2. (x + h)和x之间的差分称为前向差分,在(x + h)和(x − h)之间的差分。因为这种计算方法以x为中心,计算它左右两边的差分,所以也称为中心差分,中心差分误差更小些
上述函数是一个典型的高阶函数。
如上所示,利用微小的差分求导数的过程称为数值微分。而基于数学式的推导求导数的过程,则用“解析性” (analytic)一词,称为“解析性求解”或者“解析性求导”。比如,y = x^2 的导数,可以通过 dy/dx = 2x。
解析性求导得到的导数是不含误差的“真的导数”。
梯度法
计算梯度的代码实现:
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形状相同的数组
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([ 6., 8.])在梯度法中,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。像这样,通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法(gradient method)。梯度法是解决机器学习中最优化问题的常用方法,特别是在神经网络的学习中经常被使用。
梯度法求最小值的代码实现:
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
# lr = 0.1
for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad # 每次朝梯度方向前进,前进的步长会随着梯度的变小而变小
return x, np.array(x_history)学习率
学习率过大或者过小都无法得到好的结果,学习率过大的话,会发散成一个很大的值;反过来,学习率过小的话,基本上没怎么更新就结束了
像学习率这样的参数称为超参数。这是一种和神经网络的参数(权重和偏置)性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的,学习率这样的超参数则是人工设定的。一般来说,超参数需要尝试多个值,以便找到一种可以使学习顺利进行的设定。
神经网络的梯度
神经网络的学习也要求梯度。这里所说的梯度是指损失函数关于权重参数的梯度
代码实现:
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
# 上面的lambda等同于下面的函数
# def f(W):
# return net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)
# 梯度下降,这样的下降只能找到极小值,不能找到最小值
net.W -= 0.1*dW
dW = numerical_gradient(f, net.W)
net.W -= 0.1*dW
dW = numerical_gradient(f, net.W)
net.W -= 0.1*dW
dW = numerical_gradient(f, net.W)
net.W -= 0.1*dW
dW = numerical_gradient(f, net.W)上述的代码是求当输入值是x,目标值时t时,初始权重关于损失函数的梯度。
学习算法的实现
神经网络的学习分成下面4个步骤。
步骤1(mini-batch)
从训练数据中随机选出一部分数据,这部分数据称为mini-batch。我们的目标是减小mini-batch的损失函数的值。
步骤2(计算梯度)
为了减小mini-batch的损失函数的值,需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。
步骤3(更新参数)
将权重参数沿梯度方向进行微小更新
步骤4(重复)
重复步骤1、步骤2、步骤3。
这个方法通过梯度下降法更新参数,不过因为这里使用的数据是随机选择的mini batch数据,所以又称为随机梯度下降法(stochastic gradient descent)。随机梯度下降法一般由一个名为SGD的函数来实现
epoch是一个单位。一个epoch表示学习中所有训练数据均被使用过一次时的更新次数。比如,对于10000笔训练数据,用大小为100笔数据的mini-batch进行学习时,重复随机梯度下降法100次,所有的训练数据就都被“看过”了 。此时,100次就是一个epoch
代码实现:
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 1000 # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
#grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]第5章 误差反向传播法
本章希望大家通过计算图,直观地理解误差反向传播法
• 通过使用计算图,可以直观地把握计算过程。
• 计算图的节点是由局部计算构成的。局部计算构成全局计算。
• 计算图的正向传播进行一般的计算。通过计算图的反向传播,可以计算各个节点的导数。
• 通过将神经网络的组成元素实现为层,可以高效地计算梯度(反向传播法)。
• 通过比较数值微分和误差反向传播法的结果,可以确认误差反向传播法的实现是否正确(梯度确认)。
计算图
计算图将计算过程用图形表示出来
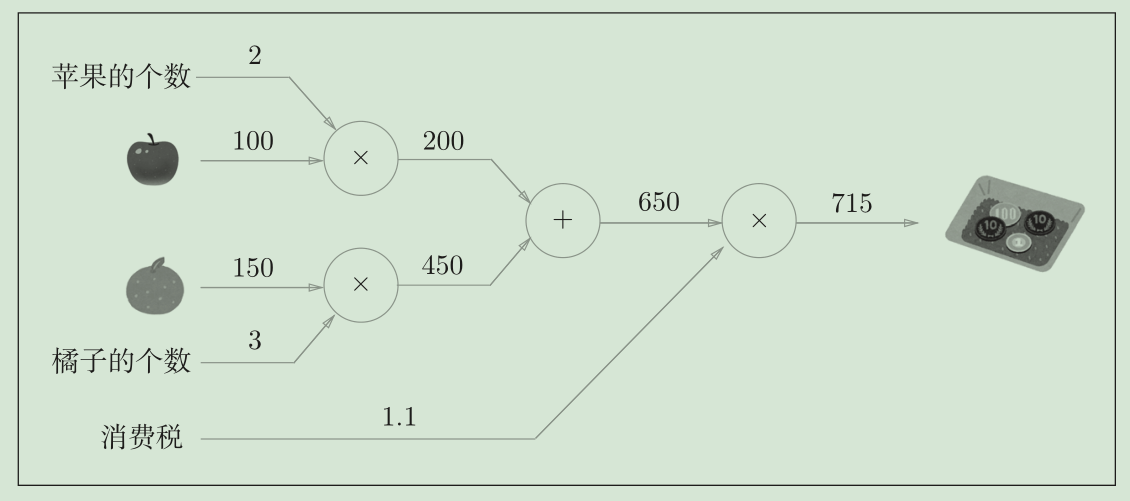
计算图的局部计算
计算图的特征是可以通过传递“局部计算”获得最终结果。“局部”这个词的意思是“与自己相关的某个小范围”。局部计算是指,无论全局发生了什么,都能只根据与自己相关的信息输出接下来的结果。
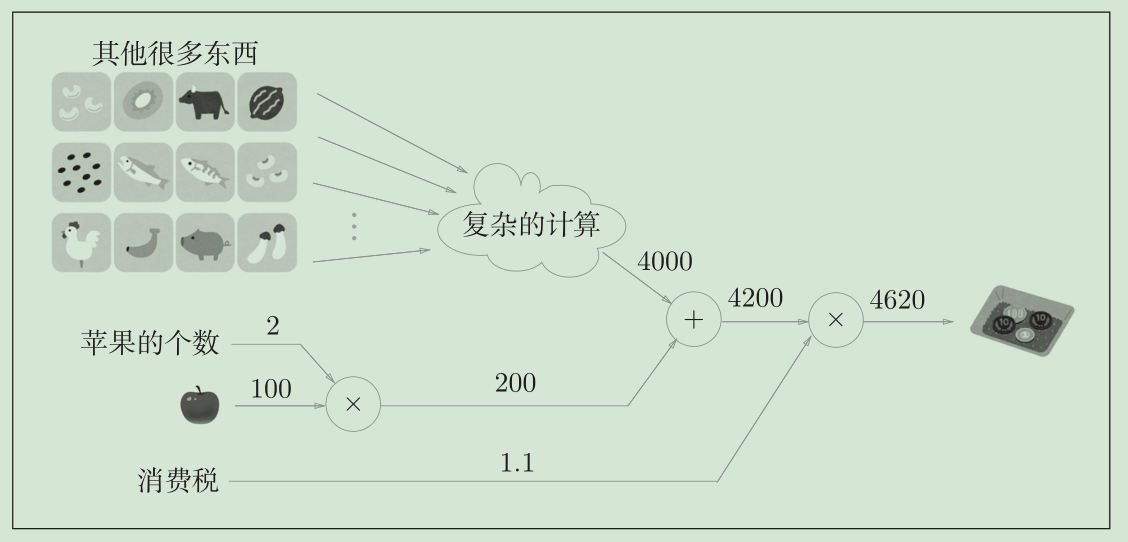
综上,计算图可以集中精力于局部计算。无论全局的计算有多么复杂,各个步骤所要做的就是对象节点的局部计算。虽然局部计算非常简单,但是通过传递它的计算结果,可以获得全局的复杂计算的结果。
另一个优点是,利用计算图可以将中间的计算结果全部保存起来
实际上,使用计算图最大的原因是,可以通过反向传播高效计算导数。
链式法则和计算图
计算图的反向传播从右到左传播信号。反向传播的计算顺序是,先将节点的输入信号乘以节点的局部导数(偏导数),然后再传递给下一个节点。最右边的节点的输入信号为dz/dz = 1

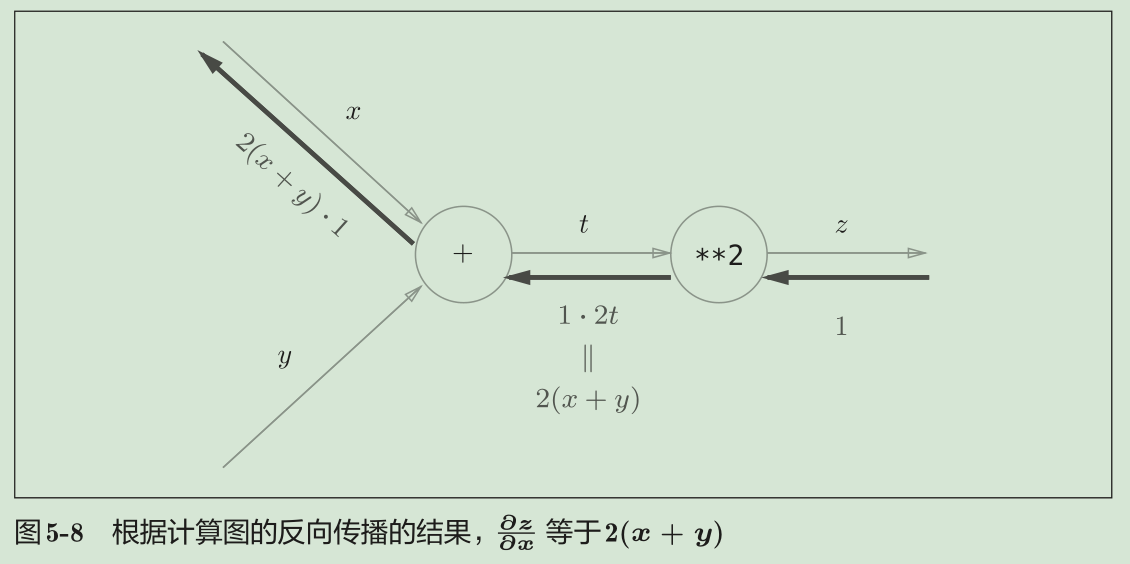
层/节点的实现
乘法层和加法层
这里我们把要实现的计算图的乘法节点称为“乘法层” ( MulLayer ),加法节点称为“加法层”( AddLayer )
层的实现中有两个共通的方法(接口) forward() 和 backward()
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy激活函数层-ReLU层
当大于0时,反向传播时原样返回,小于等于0时不返回0
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx激活函数层-Sigmoid层
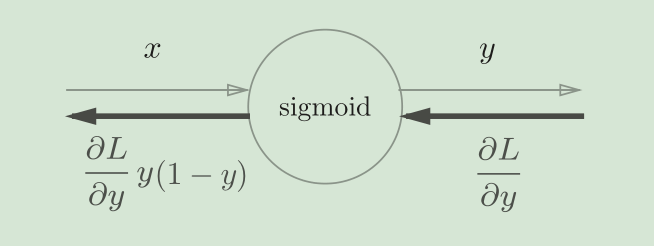
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dxAffine层
神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算。神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”。因此,这里将进行仿射变换的处理实现为“Affine层”。
几何中,仿射变换包括一次线性变换和一次平移,分别对应神经网络的加权和运算与加偏置运算。
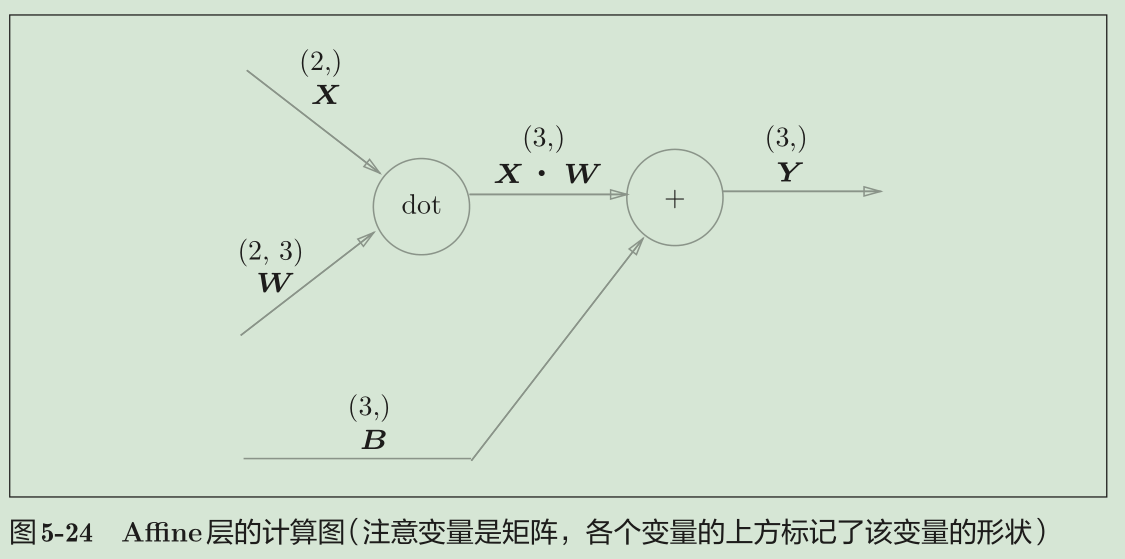


批版本的Affine层
代码实现:
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
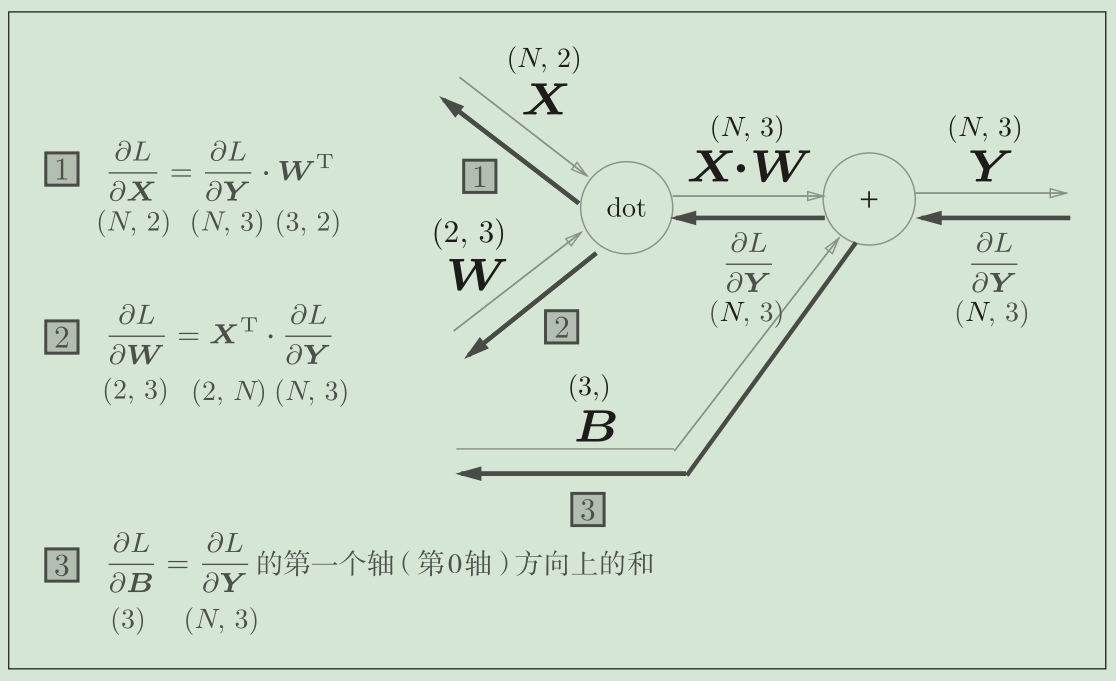
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dxSoftmax-with-Loss层
softmax函数会将输入值正规化之后再输出
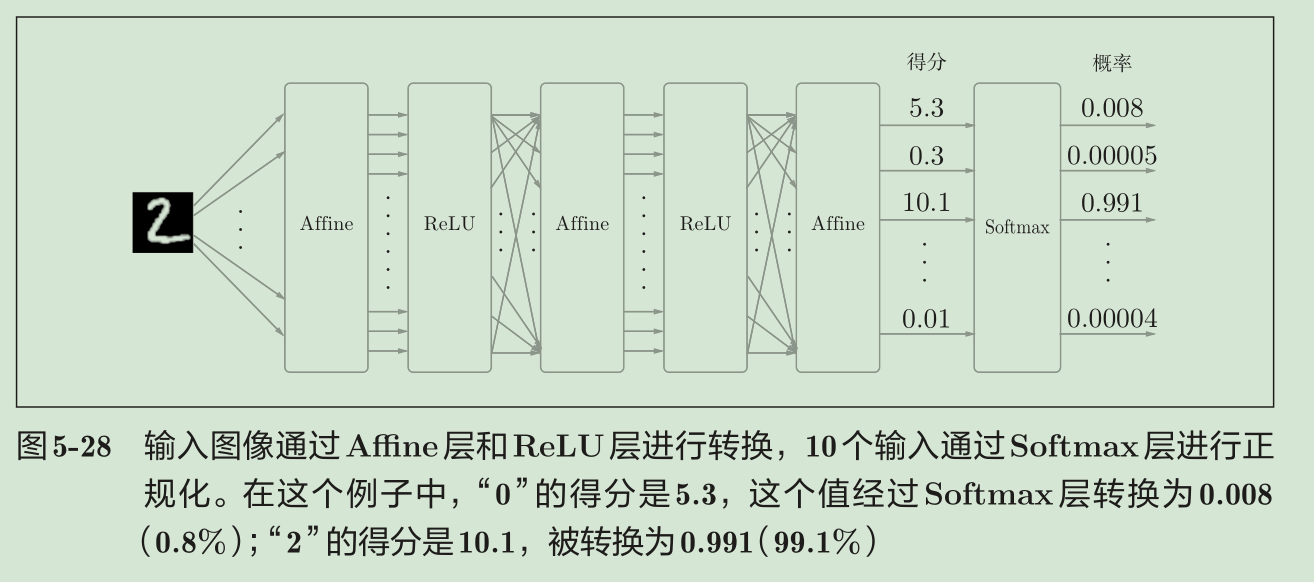
神经网络中进行的处理有推理(inference)和学习两个阶段。神经网络的推理通常不使用Softmax层。
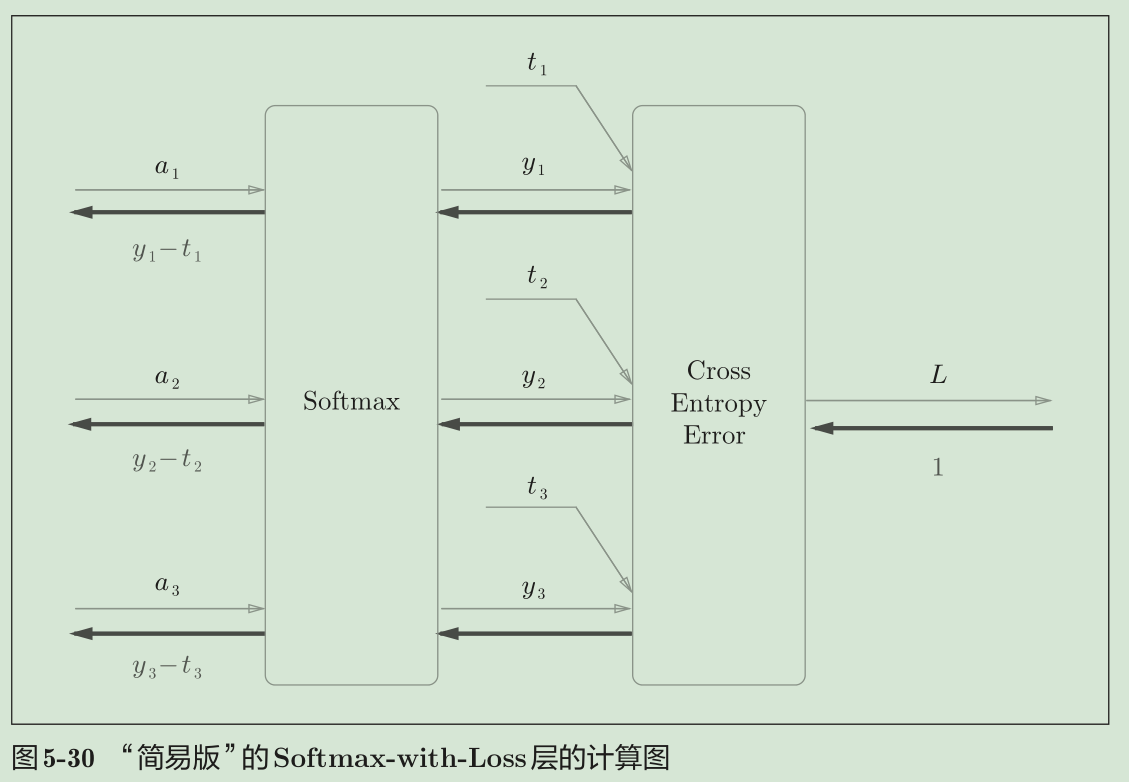
Softmax层的反向传播得到了(y1 − t1 , y2 − t2 , y3 − t3 )这样“漂亮”的结果。由于(y1 ,y2 ,y3 )是Softmax层的
输出,(t1 , t2 , t3 )是监督数据,所以(y1 − t1 ,y2 − t2 ,y3 − t3 )是Softmax层的输出和教师标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层,这是神经网络学习中的重要性质
使用交叉熵误差作为softmax函数的损失函数后,反向传播得到(y1 − t1 , y2 − t2 , y3 − t3 )这样 “漂亮”的结果。实际上,这样“漂亮”的结果并不是偶然的,而是为了得到这样的结果,特意设计了交叉熵误差函数。回归问题中输出层使用“恒等函数”,损失函数使用“平方和误差”,也是出于同样的理由(3.5节)。也就是说,使用“平方和误差”作为“恒等函数”的损失函数,反向传播才能得到(y1 −t1 ,y2 − t2 , y3 − t3 )这样“漂亮”的结果
代码实现:
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 损失
self.y = None # softmax的输出
self.t = None # 监督数据(one-hot vector)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx误差反向传播法的实现
代码实现:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict() # OrderedDict 有序字典,“有序”是指它可以记住向字典里添加元素的顺序
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads像这样通过将神经网络的组成元素以层的方式实现,可以轻松地构建神经网络。这个用层进行模块化的实现具有很大优点。因为想另外构建一个神经网络(比如5层、10层、20层……的大的神经网络)时,只需像组装乐高积木那样添加必要的层就可以了。之后,通过各个层内部实现的正向传播和反向传播,就可以正确计算进行识别处理或学习所需的梯度。
误差反向传播法的梯度确认
到目前为止,我们介绍了两种求梯度的方法。一种是基于数值微分的方法,另一种是解析性地求解数学式的方法。后一种方法通过使用误差反向传播法,即使存在大量的参数,也可以高效地计算梯度。
数值微分的优点是实现简单,因此,一般情况下不太容易出错。而误差反向传播法的实现很复杂,容易出错。所以,经常会比较数值微分的结果和误差反向传播法的结果,以确认误差反向传播法的实现是否正确。确认数值微分求出的梯度结果和误差反向传播法求出的结果是否一致(严格地讲,是非常相近)的操作称为梯度确认(gradient check)。
代码实现:
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
x_batch = x_train[:3]
t_batch = t_train[:3]
grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)
for key in grad_numerical.keys():
diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )
print(key + ":" + str(diff))第6章 与学习相关的技巧
本章介绍了神经网络的学习中的几个重要技巧。参数的更新方法、权重初始值的赋值方法、Batch Normalization、Dropout等,这些都是现代神经网络中不可或缺的技术。另外,这里介绍的技巧,在最先进的深度学习中也被频繁使用。
• 参数的更新方法,除了SGD之外,还有Momentum、AdaGrad、Adam等方法。
• 权重初始值的赋值方法对进行正确的学习非常重要。
• 作为权重初始值,Xavier初始值、He初始值等比较有效。
• 通过使用Batch Normalization,可以加速学习,并且对初始值变得健壮。
• 抑制过拟合的正则化技术有权值衰减、Dropout等。
• 逐渐缩小“好值”存在的范围是搜索超参数的一个有效方法。
参数的更新
SGD
class SGD:
"""随机梯度下降法(Stochastic Gradient Descent)"""
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
network = TwoLayerNet(...)
optimizer = SGD() # optimizer可以进行策略的替换
for i in range(10000):
...
x_batch, t_batch = get_mini_batch(...) # mini-batch
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params, grads)
...SGD的缺点
Momentum
AdaGrad
Adam
使用哪种更新方法呢
基于MNIST数据集的更新方法的比较
6.2 权重的初始值
可以将权重初始值设为0吗
隐藏层的激活值的分布
ReLU的权重初始值
基于MNIST数据集的权重初始值的比较
6.3 Batch Normalization
Batch Normalization的算法
Batch Normalization的评估
6.4 正则化
过拟合
权值衰减
Dropout
6.5 超参数的验证
验证数据
超参数的最优化
超参数最优化的实现
第7章 卷积神经网络
7.1 整体结构
7.2 卷积层
全连接层存在的问题
卷积运算
填充
步幅
3维数据的卷积运算
结合方块思考
批处理
7.3 池化层
7.4 卷积层和池化层的实现
4维数组
基于im2col的展开
卷积层的实现
池化层的实现
7.5 CNN的实现
7.6 CNN的可视化
第1层权重的可视化
基于分层结构的信息提取
7.7 具有代表性的CNN
LeNet
AlexNet
第8章 深度学习 260
8.1 加深网络
向更深的网络出发
进一步提高识别精度
加深层的动机
8.2 深度学习的小历史
ImageNet
VGG
GoogLeNet
ResNet
8.3 深度学习的高速化
需要努力解决的问题
基于GPU的高速化
分布式学习
运算精度的位数缩减
8.4 深度学习的应用案例
物体检测
图像分割
图像标题的生成
8.5 深度学习的未来
图像风格变换
图像的生成 285
自动驾驶
Deep Q-Network(强化学习)