Table of Contents:

点乘

点乘等于向量大小与向量夹角的cos值的积。点乘结果越大两向量越近

叉乘

1.叉乘的结果是垂直于两个向量所在平面的向量
2.叉乘的模可以计算两向量围成的平行四边形面积
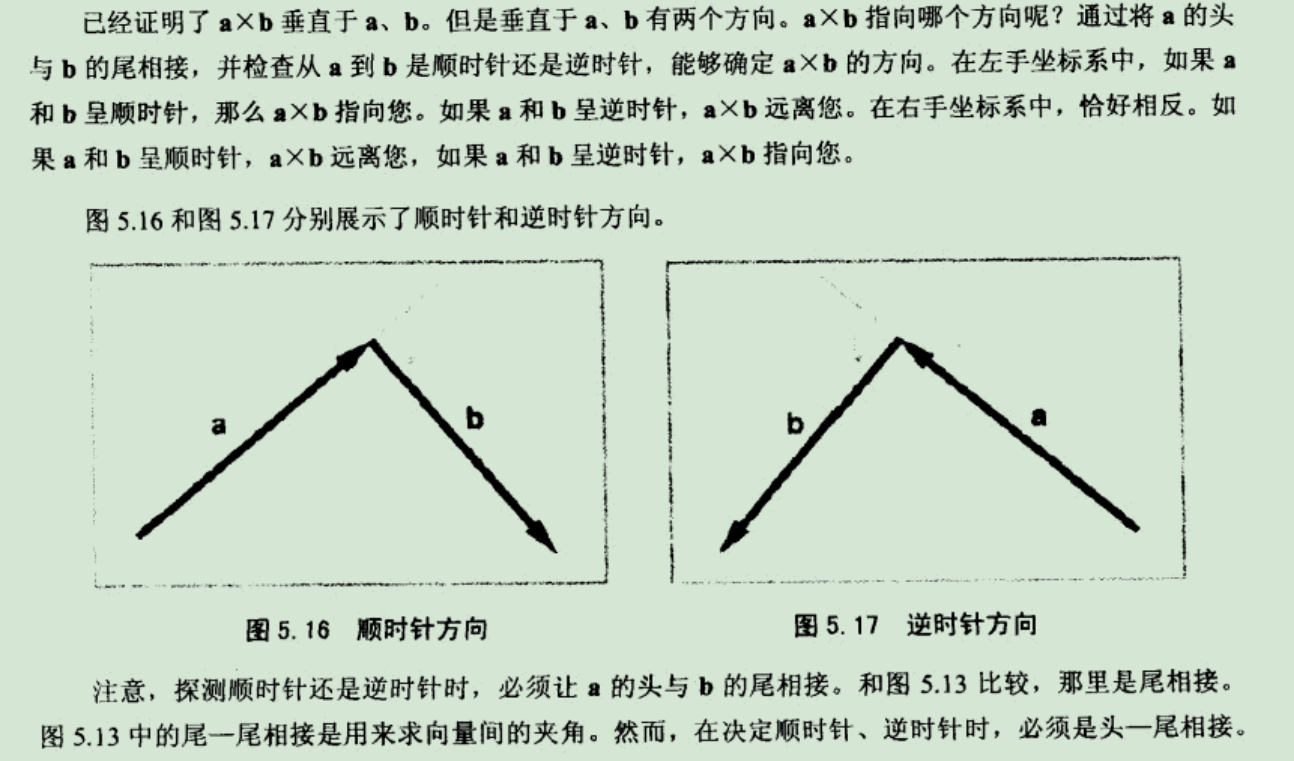
3.判断两向量顺时针和逆时针方向
4.判断点在向量的那一侧
5.判断两条线段是否交叉

在三维空间中，两个向量A=(Ax​,Ay​,Az​) 和B=(Bx​,By​,Bz​) 的叉乘（cross product）结果是一个新的向量C=A×B，其各个分量的计算公式如下：
Cx​=Ay​⋅Bz​−Az​⋅By​
Cy​=Az​⋅Bx​−Ax​⋅Bz​
Cz​=Ax​⋅By​−Ay​⋅Bx​

2d向量叉乘

假设有两个2d向量a,b，我们直接把他们视为3d向量，z轴补0，那么这个时候的a，b向量的叉乘结果c, c.x=0,c.y=0,c.z=a.x*b.y-b.x*a.y, 也就是x和y的分量为0，z的分量为a.x*b.y-b.x*a.y

这个时候可以吧2d的叉乘值定义为得到一个值，而不是得到一个向量，那么这个值k， k = c.z=a.x*b.y-b.x*a.y，我们可以通过这个k值得到很多有用的性质
如果k>0，z方向为正方向，a,b为顺时针
如果k<0，z方向为负方向，a,b为逆时针
（P叉乘Q）P^Q>0说明P在Q的顺时针方向，<0说明P在Q的逆时针方向，=0说明P和Q共线。

image.png
#include <iostream>

struct Point {
    double x, y;
};

double crossProduct(Point a, Point b, Point c) {
    // 计算向量AB和AC的叉积
    return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}

int main() {
    Point a = {1, 1};
    Point b = {8, 8};
    
    Point p = {5, 3};  // 待判断的点P

    double cross = crossProduct(a, b, p);

    if (cross > 0) {
        std::cout << "Point is on the left side of the line." << std::endl;
    } else if (cross < 0) {
        std::cout << "Point is on the right side of the line." << std::endl;
    } else {
        std::cout << "Point is on the line." << std::endl;
    }

    return 0;
}

判断两条线段是否交叉

//叉积 ac×bc, a在bc那一侧
double mult(Point a, Point b, Point c)
{
    return (a.x - c.x) * (b.y - c.y) - (b.x - c.x) * (a.y - c.y);
}

#define max( a, b ) ((a)>(b)?(a):(b))
#define min( a, b ) ((a)>(b)?(b):(a))
//aa, bb为一条线段两端点 cc, dd为另一条线段的两端点 相交返回true, 不相交返回false  
bool intersect(Point aa, Point bb, Point cc, Point dd)
{
    if (max(aa.x, bb.x) < min(cc.x, dd.x))
    {
        return false;
    }
    if (max(aa.y, bb.y) < min(cc.y, dd.y))
    {
        return false;
    }
    if (max(cc.x, dd.x) < min(aa.x, bb.x))
    {
        return false;
    }
    if (max(cc.y, dd.y) < min(aa.y, bb.y))
    {
        return false;
    }
    // cd的两点都在ab同侧
    if (mult(cc, bb, aa) * mult(dd, bb, aa) > 0)
    {
        return false;
    }
    // ab的两点都在cd同侧
    if (mult(aa, dd, cc) * mult(bb, dd, cc) > 0)
    {
        return false;
    }
    return true;
}

归一化

标准向量等于向量除以它的模，意义是简化操作只考虑向量的方向，不考虑大小