 忧郁的大能猫
忧郁的大能猫
好奇的探索者,理性的思考者,踏实的行动者。
blog/B-学科/数理化/离散数学/离散数学
Table of Contents:
集合
关系
函数
代数系统
抽象代数
抽象代数主要研究对象是代数结构,包括群、环、域、向量空间。
代数主要研究的是运算规则。一门代数, 其实都是从某种具体的运算体系中抽象出一些基本规则,建立一个公理体系,然后在这基础上进行研究。一个集合再加上一套运算规则,就构成一个代数结构1。
抽象代数将初等代数的一些概念延伸。
1. 数 –> 集合
2. + –> 二元运算
加减乘除都叫二元运算(二元指的是两个操作数)
3. 0/1 –> 单位元
0和1被抽象成单位元(identity elements),0为加法单位元,1为乘法单位元。单位元是集合的一个特殊元素(跟二元运算有关),满足单位元与其他元素相结合时,不改变该元素,即满足a ∗ e = a 与 e ∗ a = a。
4. 负数 –> 逆元素
负数推广到逆元素(inverse element),对于加法,a的逆元素是-a;对于乘法,a的逆元素是倒数1/a。直观地说,逆元可以撤销操作,如加了一个数a,再加上该数的逆元-a(相当于撤消操作),结果还是一样。
5. 结合律
结合律(Associative property)是某些二元运算的性质,有些二元运算没有结合律(如减法、除法、八元数)。
6. 交换律
交换律(Commutative property),改变二元运算符两边的元素不影响结果。并不是所有二次元运算都满足交换律(如矩阵的乘法)
群论
群 = 集合+运算
我们可以认为一个群代表了“某一类”变换。比如下面这个群:
A={-270,-180,-90,0,90,180,270}, Q=(A,)。群里的元素旋转角度,ab代表先旋转a度,再旋转b度。
群的定义:封结幺逆
- 封闭性:两个群元相乘后仍然是群元
我们可以认为一个群代表了“某一类”变换,这些变换的叠加(群乘法 )也属于“同一类”。 - 结合律
结合律可以理解为连续操作的唯一性。
如果以 {剪刀, 石头, 布} 构成一个集合,并且按照胜负规则定义所谓的乘法:
剪刀·石头=石头·剪刀=石头;
石头·布=布·石头=布;
布·剪刀=剪刀·布=剪刀
那么我们可以验证这个“乘法”不满足结合律,比如:
石头·(布·剪刀)=石头·剪刀=石头,而:
(石头·布)·剪刀=布·剪刀=剪刀
这样的乘法本身就是“畸形”的,因为它无法定义唯一的“连续操作”。 - 幺元存在性
幺元很好理解,就是“什么都不做”的变换。即乘以幺元后元素不变。 - 逆元存在性
逆元也很好理解,就是“做了又反悔”的变换。即乘以后得到了幺元。
逆元存在性意味着允许群元“悔棋”,否则构不成群,只能构成半群,因为每个群元都找不到自己的另一半。
代数结构(R, *),二元运算根据封闭性、单位元、逆元、结合律、交换律,可以归纳成不同的群。从最不严格到严格(依次添加限制条件),其关系图如下:
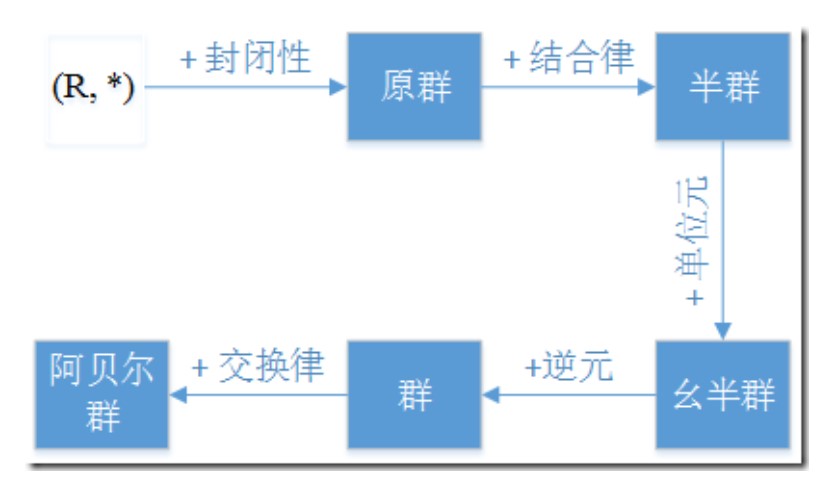
- 原群(magma)
是一种基本的代数结构,只要满足两元素作二元运算得到新元素仍属于该集合,即封闭性。 - 半群(Semigroup)
满足结合律(associative property)的代数结构。V=<S,* >,其中二元运算*是可结合的,即(a*b)*c=a*(b*c),则称V是半群。 - 幺半群(monoid)
在半群的基础上,还需要满足有一个单位元 - 群(group)
在幺半群基础上再加上逆元,如整数集合,二次元运算为加法就是一个群(封闭性是显然的,加法满足结合律,单位元为0,逆元取相反数-a。 - 阿贝尔群(交换群)(Abelian Group)
在群的基础上,还需满足交换律。如整数集合和加法运算,(Z,+),是一个阿贝尔群。
环论
环在交换群基础上,进一步限制条件。环、交换环、域间的关系如下:

环(ring)
在阿贝尔群(也叫交换群)的基础上,添加一种二元运算·(虽叫乘法,但不同于初等代数的乘法)。一个代数结构是环(R, +, ·)。需要满足环公理(ring axioms),如(Z,+, ⋅)。环公理如下
1. (R, +)是交换群
2. (R, ·)是幺半群
3. 乘法对加法满足分配律
交换环(commutative ring)
交换环(commutative ring)在环的基础上,二元运算乘法还满足交换律。
整环(integral domain)
在交换环的基础上,并满足没有零因子(如此,集合内任意两个元素乘积均不等于0)
域
域(Field)在交换环的基础上,还增加了二元运算除法,要求元素(除零以外)可以作除法运算,即每个非零的元素都要有乘法逆元。由此可见,域是一种可以进行加减乘除(除0以外)的代数结构,是数域与四则运算的推广。整数集合,不存在乘法逆元(1/3不是整数),所以整数集合不是域。有理数、实数、复数可以形成域,分别叫有理数域、实数域、复数域。
向量空间
向量空间(vector space)是一些向量的集合。其他例子,还包括坐标空间(Coordinate spaces)、复数、函数空间(Function spaces)、线性方程组(linear equations)。
模
模(module)是对向量空间的推广,将标量需为域(向量空间)推广到任意环(模)。
格
格(lattice)是任意两个元素都有上确界和下确界的偏序集合。