忧郁的大能猫

好奇的探索者，理性的思考者，踏实的行动者。

Table of Contents:

01 | 二进制：不了解计算机的源头，你学什么编程

Java 里定义了两种右移，逻辑右移(无符号移位)和算术右移(有符号的移位操作)
* 逻辑右移： 右移1 位，左边补 0 即可
* 算术右移：移动时保持符号位不变，就是将补码右移并在空出来的地方填充符号位，这样做的目的就是利用补码的规则实现右移一位等效于数值缩小一倍，比如-3变为-1，-2变为-1，而-1比较特殊，右移还是-1

逻辑右移在 Java 和 Python 语言中使用 >>> 表示，而算术右移使用 >> 表示。

在 C 或 C++ 语言中，逻辑右移和算数右移共享同一个运算符 >>。那么，编译器是如何决定使用逻辑右移还是算数右移呢？答案是，取决于运算数的类型。如果运算数类型是 unsigned，则采用逻辑右移；而是 signed，则采用算数右移。如果你针对 unsigned 类型的数据使用算数右移，或者针对 signed 类型的数据使用逻辑右移，那么你首先需要进行类型的转换。

位的“异或”
相同的为0，不同为1. 一个二进制数和自身异或后为所有都为0

02 | 余数：原来取余操作本身就是个哈希函数

同余定理：简单来说，就是两个整数 a 和 b，如果它们除以正整数 m 得到的余数相等，我们就可以说 a 和 b 对于模 m 同余

我们经常提到的奇数和偶数，其实也是同余定理的一个应用。当然，这个应用里，它的模就是 2 了，2 除以 2 余 0，所以它是偶数；3 除以 2 余 1，所以它是奇数。2 和 4 除以 2 的余数都是 0，所以它们都是一类，都是偶数。3 和 5 除以 2 的余数都是 1，所以它们都是一类，都是奇数。

简单来说，同余定理其实就是用来均分的。你知道，我们有无穷多个整数，那怎么能够全面、多维度地管理这些整数？同余定理就提供了一个思路。

因为不管你的模是几，最终得到的余数肯定都在一个范围内。比如我们上面除以 7，就得到了星期几；我们除以 2，就得到了奇偶数。所以按照这种方式, 我们就可以把无穷多个整数分成有限多个类。

03 | 迭代法：不用编程语言的自带函数，你会如何计算平方根？

迭代法是如何通过重复的步骤进行计算或者查询的

1. 求方程的精确或者近似解

假设有正整数 n，这个平方根一定小于 n 本身，并且大于 1。那么这个问题就转换成，在 1 到 n 之间，找一个数字等于 n 的平方根。

我这里采用迭代中常见的二分法。每次查看区间内的中间值，检验它是否符合标准。

public static double getSqureRoot(int n, double deltaThreshold, int maxTry) {
 
 if (n <= 1) {
  return -1.0;
 }
 
 double min = 1.0, max = (double)n;
 for (int i = 0; i < maxTry; i++) {
  double middle = (min + max) / 2;
  double square = middle * middle;
  double delta = Math.abs((square / n) - 1);
  if (delta <= deltaThreshold) {
   return middle;
  } else {
   if (square > n) {
 max = middle;
   } else {
 min = middle;
   }
  }
 }
 
 return -2.0;


}

2. 查找匹配记录

二分查找法

04 | 数学归纳法：如何用数学归纳提升代码的运行效率？

迭代法是如何通过重复的步骤进行计算或者查询的。与此不同的是，数学归纳法在理论上证明了命题是否成立，而无需迭代那样反复计算，因此可以帮助我们节约大量的资源，并大幅地提升系统的性能。

迭代把计算交给计算机，归纳把计算交给人，前者是拿计算机的计算成本换人的时间，后者是拿人的时间换计算机的计算成本

在数论中，数学归纳法用来证明任意一个给定的情形都是正确的，也就是说，第一个、第二个、第三个，一直到所有情形，概不例外。

数学归纳法的一般步骤是这样的：
* 证明当n= 1时命题成立。
* 假设n=m时命题成立，那么可以推导出在n=m+1时命题也成立。（m代表任意自然数）

第一个子命题是，第 n 个棋格放的麦粒数为 2^(n−1)
我们来证明第一个子命题。

• 基本情况：我们已经验证了 n=1 的时候，第一格内的麦粒数为 1，和 21−1 相等。因此，命题在 k=1 的时候成立。

• 假设第 k−1 格的麦粒数为 2^(k−2)。那么第 k 格的麦粒数为第 k−1 格的 2 倍，也就是 2^{(k−2)∗2=2}(k−1)。因此，如果命题在 k=n−1 的时候成立，那么在 k=n 的时候也成立。

和使用迭代法的计算相比，数学归纳法最大的特点就在于“归纳”二字。它已经总结出了规律。只要我们能够证明这个规律是正确的，就没有必要进行逐步的推算，可以节省很多时间和资源。

05 | 递归（上）：泛化数学归纳，如何将复杂问题简单化？

假设有四种面额的钱币，1 元、2 元、5 元和 10 元，而您一共给我 10 元，那您可以奖赏我 1 张 10 元，或者 10 张 1 元，或者 5 张 1 元外加 1 张 5 元等等。如果考虑每次奖赏的金额和先后顺序，那么最终一共有多少种不同的奖赏方式呢？”

虽然迭代法的思想是可行的，但是如果用循环来实现，恐怕要保存好多中间状态及其对应的变量。说到这里，你是不是很容易就想到计算编程常用的函数递归？

在递归中，每次嵌套调用都会让函数体生成自己的局部变量，正好可以用来保存不同状态下的数值，为我们省去了大量中间变量的操作，极大地方便了设计和编程。

public class Lesson5_1 {
    
 public static long[] rewards = {1, 2, 5, 10}; // 四种面额的纸币
    
 /**
    * @Description: 使用函数的递归（嵌套）调用，找出所有可能的奖赏组合
    * @param totalReward- 奖赏总金额，result- 保存当前的解
    * @return void
    */
    
    public static void get(long totalReward, ArrayList<Long> result) {
     
     // 当 totalReward = 0 时，证明它是满足条件的解，结束嵌套调用，输出解
     if (totalReward == 0) {
      System.out.println(result);
      return;
     }
     // 当 totalReward < 0 时，证明它不是满足条件的解，不输出
     else if (totalReward < 0) {
      return;
     } else {
      for (int i = 0; i < rewards.length; i++) {
       ArrayList<Long> newResult = (ArrayList<Long>)(result.clone()); // 由于有 4 种情况，需要 clone 当前的解并传入被调用的函数
       newResult.add(rewards[i]); // 记录当前的选择，解决一点问题
       get(totalReward - rewards[i], newResult); // 剩下的问题，留给嵌套调用去解决
      }
     }
     
    }
 
}

这里从奖赏的总金额开始，每次嵌套调用的时候减去一张纸币的金额，直到所剩的金额为 0 或者少于 0，然后结束嵌套调用，开始返回结果值。当然，你也可以反向操作，从金额 0 开始，每次嵌套调用的时候增加一张纸币的金额，直到累计的金额达到或超过总金额。

递归和循环其实都是迭代法的实现，而且在某些场合下，它们的实现是可以相互转化的。但是，对于某些应用场景，递归确很难被循环取代。我觉得主要有两点原因：

第一，递归的核心思想和数学归纳法类似，并更具有广泛性。这两者的类似之处体现在：将当前的问题化解为两部分：一个当前所采取的步骤和另一个更简单的问题。
1. 一个当前所采取的步骤。这种步骤可能是进行一次运算（例如每个棋格里的麦粒数是前一格的两倍），或者做一个选择（例如选择不同面额的纸币），或者是不同类型操作的结合（例如今天讲的赏金的案例）等等。
2. 另一个更简单的问题。经过上述步骤之后，问题就会变得更加简单一点。这里“简单一点”，指运算的结果离目标值更近（例如赏金的总额），或者是完成了更多的选择（例如纸币的选择）。而“更简单的问题”，又可以通过嵌套调用，进一步简化和求解，直至达到结束条件。

我们只需要保证递归编程能够体现这种将复杂问题逐步简化的思想，那么它就能帮助我们解决很多类似的问题。

第二，递归会使用计算机的函数嵌套调用。而函数的调用本身，就可以保存很多中间状态和变量值，因此极大的方便了编程的处理。

06 | 递归（下）：分而治之，从归并排序到MapReduce

归并排序使用了分治的思想，而这个过程需要使用递归来实现。

当需要排序的数组很大（比如达到 1024GB 的时候），我们没法把这些数据都塞入一台普通机器的内存里。该怎么办呢？有一个办法，我们可以把这个超级大的数据集，分解为多个更小的数据集（比如 16GB 或者更小），然后分配到多台机器，让它们并行地处理。

等所有机器处理完后，中央服务器再进行结果的合并。由于多个小任务间不会相互干扰，可以同时处理，这样会大大增加处理的速度，减少等待时间。
在单台机器上实现归并排序的时候，我们只需要在递归函数内，实现数据分组以及合并就行了。而在多个机器之间分配数据的时候，递归函数内除了分组及合并，还要负责把数据分发到某台机器上。

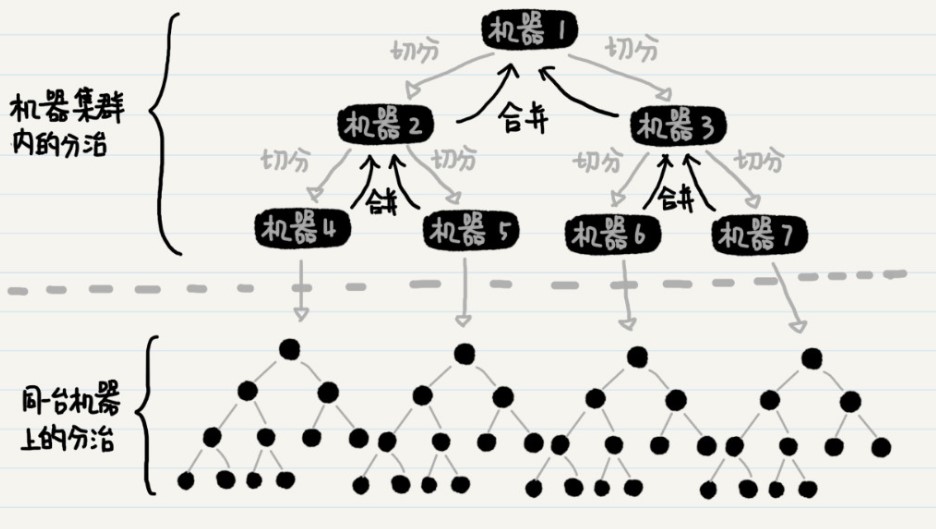
在这个框架图中，你应该可以看到，分布式集群中的数据切分和合并，同单台机器上归并排序的过程是一样的，因此也是使用了分治的思想。从理论的角度来看，上面这个图很容易理解。不过在实际运用中，有个地方需要注意一下。

07 | 排列：如何让计算机学会“田忌赛马”？

1. 从n个不同的元素中取出m（1<=m<=n）个不同的元素，按照一定的顺序排成一列，这个过程就叫做排列。当m=n的时候这就是全排列。
2. 排列可以琼剧出随机变量取值的所有可能性，所以他在概率中有很大作用，比如用于生成保额份额变量的概率分布。排列在计算机领域也有很多应用场景，比如暴力破解。

排列可以帮助我们生成很多可能性。由于这种特性，排列最多的用途就是穷举法，也就是，列出所有可能的情况，一个一个验证，然后看每种情况是否符合条件的解。

古代的孙膑利用排列的思想，穷举了田忌马匹的各种出战顺序，然后获得了战胜齐王的策略。现代的黑客，通过排列的方法，穷举了各种可能的密码，试图破坏系统的安全性。如果你所面临的问题，它的答案也是各种元素所组成的排列，那么你就可以考虑，有没有可能排列出所有的可能性，然后通过穷举的方式来获得最终的解。

08 | 组合：如何让计算机安排世界杯的赛程？

1.组合是指，从n个不同的元素中取出m（1<=m<=n）个不同的元素。所有m取值的组合之全集合叫做全组合。

09 | 动态规划（上）：如何实现基于编辑距离的查询推荐？

那什么是动态规划呢？在递归那一节，我说过，我们可以通过不断分解问题，将复杂的任务简化为最基本的小问题，比如基于递归实现的归并排序、排列和组合等。不过有时候，我们并不用处理所有可能的情况，只要找到满足条件的最优解就行了。在这种情况下，我们需要在各种可能的局部解中，找出那些可能达到最优的局部解，而放弃其他的局部解。这个寻找最优解的过程其实就是动态规划。

动态规划需要通过子问题的最优解，推导出最终问题的最优解，因此这种方法特别注重子问题之间的转移关系。我们通常把这些子问题之间的转移称为状态转移，并把用于刻画这些状态转移的表达式称为状态转移方程。很显然，找到合适的状态转移方程，是动态规划的关键。

编辑距离

当你在搜索引擎的搜索框中输入单词的时候，有没有发现，搜索引擎会返回一系列相关的关键词，方便你直接点击。甚至，当你某个单词输入有误的时候，搜索引擎依旧会返回正确的搜索结果。
搜索下拉提示和关键词纠错，这两个功能其实就是查询推荐。查询推荐的核心思想其实就是，对于用户的输入，查找相似的关键词并进行返回。而测量拉丁文的文本相似度，最常用的指标是编辑距离（Edit Distance）。
由一个字符串转成另一个字符串所需的最少编辑操作次数，我们就叫作编辑距离。这个概念是俄罗斯科学家莱文斯坦提出来的，所以我们也把编辑距离称作莱文斯坦距离（Levenshtein distance）。很显然，编辑距离越小，说明这两个字符串越相似，可以互相作为查询推荐。编辑操作有这三种：把一个字符替换成另一个字符；插入一个字符；删除一个字符。
比如，我们想把 mouuse 转换成 mouse，有很多方法可以实现，但是很显然，直接删除一个“u”是最简单的，所以这两者的编辑距离就是 1。

10 | 动态规划（下）：如何求得状态转移方程并进行编程实现？

11 | 树的深度优先搜索（上）：如何才能高效率地查字典？

12 | 树的深度优先搜索（下）：如何才能高效率地查字典？

这两节讲的主要是数据结构和算法的知识，跟数学关系不大